题目内容
【题目】如图，在正方体ABCD－A1B1C1D1中，O为底面ABCD的中心，P是DD1的中点，设Q是CC1上的点，问：当点Q在什么位置时，平面D1BQ与平面PAO平行？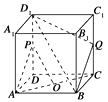
【答案】解：如图，设平面D1BQ∩平面ADD1A1＝D1M，点M在AA1上，由于平面D1BQ∩平面BCC1B1＝BQ，平面ADD1A1∥平面BCC1B1 ， 所以由面面平行的性质定理可得BQ∥D1M.
因为平面D1BQ∥平面PAO，平面D1BQ∩平面ADD1A1＝D1M，平面PAO∩平面ADD1A1＝AP，所以AP∥D1M，所以BQ∥AP.因为P为DD1的中点，所以Q为CC1的中点．
故当Q为CC1的中点时，平面D1BQ∥平面PAO.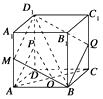
【解析】由于P是DD1的中点，当平面D1BQ与平面PAO平行时，由面面平行的性质得到BQ∥AP，从而Q为CC1的中点．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
【题目】对某校高三年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数，根据此数据作出了频数与频率的统计表和频率分布直方图.
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 24 | n |
[20,25) | m | p |
[25,30] | 2 | 0.05 |
合计 | M | 1 |
（1）求出表中M，p及图中a的值；
（2）若该校高三学生有240人，试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数；
（3）估计这次学生参加社区服务人数的众数、中位数以及平均数．
