题目内容
19.调查某医院某段时间内婴儿出生的时间与性别的关系,得到部分数据如表:| 晚上 | 白天 | 合计 | |
| 男婴 | ? | 31 | 55 |
| 女婴 | 8 | ? | 34 |
| 合计 | 32 | 57 | 89 |
| A. | 80% | B. | 90% | C. | 95% | D. | 不能确定 |
分析 根据所给的数据,代入求观测值的公式,得到观测值,把观测值同临界值进行比较得到有90%的把握认为婴儿出生的时间与性别有关系.
解答 解:由题意,2×2列联表为:
| 晚上 | 白天 | 合计 | |
| 男婴 | 24 | 31 | 55 |
| 女婴 | 8 | 26 | 34 |
| 合计 | 32 | 57 | 89 |
∴有90%的把握认为婴儿出生的时间与性别有关系.
故选:B.
点评 本题考查独立性检验的应用,本题解题的关键是理解临界值对应的概率的意义,能够看出两个变量之间的关系,本题是一个基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.若a>b>0>c,则以下不等式恒成立的是( )
| A. | $\frac{1}{a}$+$\frac{1}{b}$>$\frac{1}{ab}$ | B. | $\frac{c}{a-c}$>$\frac{c}{b-c}$ | C. | ac>bc | D. | a2+b2>c2 |
4.已知点F(c,0)(c>0)是椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1的右焦点,F关于直线y=$\frac{\sqrt{3}}{3}$x的对称点A 也在椭圆上,则该椭圆的离心率是( )
| A. | $\sqrt{3}$+2 | B. | $\sqrt{3}$-1 | C. | $\frac{\sqrt{3}-1}{2}$ | D. | -$\sqrt{3}$+2 |
11.在等差数列{an}中,an>0,且前10项和S10=30,则a5a6的最大值是( )
| A. | 3 | B. | 6 | C. | 9 | D. | 36 |
9.已知a>0,b>0,则$6\sqrt{ab}+\frac{3}{a}+\frac{3}{b}$的最小值是( )
| A. | 10 | B. | $12\sqrt{2}$ | C. | 12 | D. | 20 |
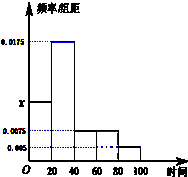 某校对新生的上学所需时间进行了统计(单位:分钟),并将所得数据绘制成频率分布直方图,(如图),其中所需时间的范围为[0,100],数据分组[0,20),[20,40),[40,60),[60,80),[80,100]
某校对新生的上学所需时间进行了统计(单位:分钟),并将所得数据绘制成频率分布直方图,(如图),其中所需时间的范围为[0,100],数据分组[0,20),[20,40),[40,60),[60,80),[80,100]