题目内容
12.设集合A={x∈N|$\frac{6}{3-x}$∈Z},B={(x,y)|x+y=3,x∈N,y∈N},则用列举法表示A={0,1,2,4,5,6,9},B={(0,3),(1,2),(2,1),(3,0)}.分析 先看集合A,由于x∈N,从而让x从0开始取值,同时还要使得$\frac{6}{3-x}$∈Z,从而可以得出x的取值,从而用列举法表示出集合A;同样的方法,对于集合B,x∈N,y∈N,从而让x从0取值,还要使得y∈N,这样得出对应的(x,y),从而列举法表示出集合B.
解答 解:对于集合A,根据x∈N,$\frac{6}{3-x}∈Z$,x可以取0,1,2,4,5,6,9;
A={0,1,2,4,5,6,9};
对于集合B,根据x∈N,y∈N,(x,y)分别为(0,3),(1,2),(2,1),(3,0);
∴B={(0,3),(1,2),(2,1),(3,0)}.
故答案为:0,1,2,4,5,6,9},{(0,3),(1,2),(2,1),(3,0)}.
点评 考查描述法、列举法表示集合,理解描述法的定义,认清描述法所表示集合的元素.

练习册系列答案
相关题目
2.已知某程序框图如图所示,则输出的i的值为( )


| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
3.某位同学设计下面的程序框图用以计算和式12+22+32+…+212的值,则在判断框中应填写( )


| A. | i≤20 | B. | i≥20 | C. | i≤22 | D. | i≤21 |
4.已知点F(c,0)(c>0)是椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1的右焦点,F关于直线y=$\frac{\sqrt{3}}{3}$x的对称点A 也在椭圆上,则该椭圆的离心率是( )
| A. | $\sqrt{3}$+2 | B. | $\sqrt{3}$-1 | C. | $\frac{\sqrt{3}-1}{2}$ | D. | -$\sqrt{3}$+2 |
1.设a∈R,则“a>1”是“$\frac{1-{a}^{2}}{a}$<1-a”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
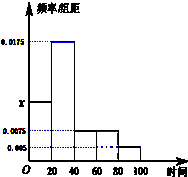 某校对新生的上学所需时间进行了统计(单位:分钟),并将所得数据绘制成频率分布直方图,(如图),其中所需时间的范围为[0,100],数据分组[0,20),[20,40),[40,60),[60,80),[80,100]
某校对新生的上学所需时间进行了统计(单位:分钟),并将所得数据绘制成频率分布直方图,(如图),其中所需时间的范围为[0,100],数据分组[0,20),[20,40),[40,60),[60,80),[80,100]