题目内容
15.如果关于x的不等式$a≤\frac{5}{9}{x^2}-\frac{10}{3}x+6≤b$的解集是[x1,x2]∪[x3,x4],x1<x2<x3<x4,则$\sum_{i=1}^4{x_i}$=12.分析 根据一元二次不等式的解集与对应一元二次方程之间的关系,利用根与系数的关系,即可求出结果.
解答 解:因为关于x的不等式a≤$\frac{5}{9}$x2-$\frac{10}{3}$x+6≤b的解集是[x1,x2]∪[x3,x4],且x1<x2<x3<x4,
所以x2,x3是方程$\frac{5}{9}$x2-$\frac{10}{3}$x+6=a的两根,
由根与系数的关系得:x2+x3=$\frac{\frac{10}{3}}{\frac{5}{9}}$=6;
x1,x4是方程$\frac{5}{9}$x2-$\frac{10}{3}$x+6=b的两根,
所以,x1+x4=$\frac{\frac{10}{3}}{\frac{5}{9}}$=6;
所以$\sum_{i=1}^{4}$xi=x1+x2+x3+x4=12.
故答案为:12.
点评 本题考查了一元二次不等式的解法与应用问题,是基础题目.

练习册系列答案
相关题目
5.已知X~N(0,σ2),且P(-2≤X<0)=0.4,则P(X>2)=( )
| A. | 0.2 | B. | 0.1 | C. | 3 | D. | 0.4 |
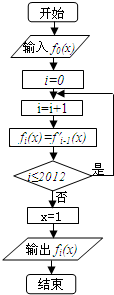
3.某位同学设计下面的程序框图用以计算和式12+22+32+…+212的值,则在判断框中应填写( )


| A. | i≤20 | B. | i≥20 | C. | i≤22 | D. | i≤21 |
4.已知点F(c,0)(c>0)是椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1的右焦点,F关于直线y=$\frac{\sqrt{3}}{3}$x的对称点A 也在椭圆上,则该椭圆的离心率是( )
| A. | $\sqrt{3}$+2 | B. | $\sqrt{3}$-1 | C. | $\frac{\sqrt{3}-1}{2}$ | D. | -$\sqrt{3}$+2 |
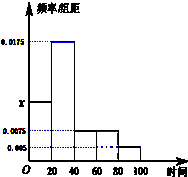 某校对新生的上学所需时间进行了统计(单位:分钟),并将所得数据绘制成频率分布直方图,(如图),其中所需时间的范围为[0,100],数据分组[0,20),[20,40),[40,60),[60,80),[80,100]
某校对新生的上学所需时间进行了统计(单位:分钟),并将所得数据绘制成频率分布直方图,(如图),其中所需时间的范围为[0,100],数据分组[0,20),[20,40),[40,60),[60,80),[80,100] 如图是函数 f(x)=Asin(ωx+φ) (A>0,ω>0,$|φ|<\frac{π}{2}$)在一个周期的图象.
如图是函数 f(x)=Asin(ωx+φ) (A>0,ω>0,$|φ|<\frac{π}{2}$)在一个周期的图象.