题目内容
1.已知{an}、{bn}都是各项均为正数且公差不为0的等差数列,满足anbn+1+an+1bn=2nan+1(n∈N*).(1)求证:数列{an}有无穷多个,而数列{bn}惟一确定;
(2)设an+1=$\frac{{2{a_n}^2+{a_n}}}{{{a_n}+1}}(n∈{N^*})$,sn=b1+b2+b3+…+b2n-1+b2n,求证:2<$\frac{S_n}{n^2}$<6.
分析 (1)通过将an=a1+(n-1)d,bn=b1+(n-1)d2代入anbn+1+an+1bn=2nan+1(n∈N*),计算即得结论;
(2)一方面通过an+1-an计算可得an<an+1,放缩可得2n<bn+1+bn,进而有Sn=$\sum_{i=1}^{2n}{b}_{i}$>2[1+3+…+(2n-1)],另一方面通过anbn+1=(2n-bn)•an+1>0,an+1>0,可得Sn=$\sum_{i=1}^{2n}{b}_{i}$<2(1+2+…+2n),计算可得结论.
解答 证明:(1)设{an}、{bn}公差分别为d1、d2(d1d2≠0),
则an=a1+(n-1)d,bn=b1+(n-1)d2,
代入anbn+1+an+1bn=2nan+1(n∈N*),
可得[a1+(n-1)d1][b1+nd2]+(a1+nd1)[b1+(n-1)d2]=2n(a1+nd1)是个恒等式,
可得$\left\{\begin{array}{l}{2{d}_{1}{d}_{2}=2{d}_{1}}\\{2{b}_{1}{d}_{1}+2{a}_{1}{d}_{2}-2{d}_{1}{d}_{2}=2{a}_{1}}\\{2{a}_{1}{b}_{1}-{b}_{1}{d}_{1}-{a}_{2}{d}_{2}=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{{d}_{1}={a}_{1}}\\{{b}_{1}=1}\\{{d}_{2}=1}\end{array}\right.$,
可得an=na1,bn=n.
∴a1可取无穷多个正实数,可得数列{an}有无穷多个,而数列{bn}惟一确定;
(2)∵an+1=$\frac{{2{a_n}^2+{a_n}}}{{{a_n}+1}}(n∈{N^*})$,
∴an+1-an=an+1=$\frac{2{{a}_{n}}^{2}+{a}_{n}}{{a}_{n}+1}$-an=$\frac{{{a}_{n}}^{2}}{{a}_{n}+1}$>0,
∴an<an+1,
∴anbn+1+an+1bn=2nan+1<an+1bn+1+an+1bn,
∴2n<bn+1+bn.
∴Sn=$\sum_{i=1}^{2n}{b}_{i}$=(b1+b2)+(b3+b4)+…+(b2n-1+b2n)>2[1+3+…+(2n-1)]=2n2.
又anbn+1=(2n-bn)•an+1>0,an+1>0,
∴2n-bn>0.
∴Sn=$\sum_{i=1}^{2n}{b}_{i}$<2(1+2+…+2n)=2n(1+2n)=4n2+2n,
∴Sn∈(2n2,4n2+2n),
∴2<$\frac{{S}_{n}}{{n}^{2}}$<4+$\frac{2}{n}$≤6.
∴$2<\frac{S_n}{n^2}<6$.
点评 本题是一道关于数列的综合题,考查运算求解能力,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.

| A. | (1,+∞) | B. | {-1}∪(1,+∞) | C. | (-∞,-1) | D. | (-∞,-1)∪(1,+∞) |
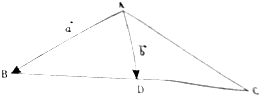 如图,在△ABC中,D为BC中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$.
如图,在△ABC中,D为BC中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$.