Question

18．如图1是一个边长为1的正三角形，分别连接这个三角形三边中点，将在三角剖分成4个三角开（如图2），再分别连接图2中一个小三角形三边的中点，又可将原三角形剖分成7个三角形（如图3），…，依此类推，设第n个图中原三角形被剖分成a_n个三角形，则第4个图中最小三角形的边长为（　　）；a₁₀₀=（　　）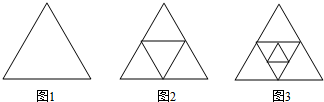

• A． $\frac{1}{6}$，300
• B． $\frac{1}{8}$，300
• C． $\frac{1}{6}$，298
• D． $\frac{1}{8}$，298

Answer 1

分析 根据图形依次求出三角形个数和最小三角形的边长，根据等差、等比数列的特点进行归纳，再利用等差、等比数列的通项公式进行求解．

解答 解：由题意得，图（1）、图（2）、图（3）中三角形被分割成1个，4个，7个；
∴三角形个数依次成等差数列，首项为1，公差为3，
∵图（1）、图（2）、图（3）中最小三角形的边长是1、$\frac{1}{2}$、$\frac{1}{4}$；
∴最小三角形的边长依次成等比数列，首项为1，公比为$\frac{1}{2}$，
∴第4个图中最小三角形的边长为1×$（\frac{1}{2}）^{3}$=$\frac{1}{8}$，
a₁₀₀=1+（100-1）×3=298，
故选：D．

点评 本题考查了归纳推理，等差、等比数列的通项公式，考查图形变化的一般规律问题，通过观察掌握其内在规律，考查学生观察、分析、归纳能力，属基础题．