题目内容
3．由抛物线y=x2与直线y=2x围成的封闭图形的面积为（ ）| A． | 8 | B． | $\frac{8}{3}$ | C． | $\frac{4}{3}$ | D． | 4 |
分析 先求曲线的交点的坐标，确定积分区间，再用定积分表示面积即可得到结论．
解答 
解：由$\left\{\begin{array}{l}{y={x}^{2}}\\{y=2x}\end{array}\right.$，可得交点的坐标为（0，0），A（2，4），
∴所求的封闭图形的面积为S=${∫}_{0}^{2}（2x-{x}^{2}）dx$=（x2-$\frac{1}{3}{x}^{3}$）${|}_{0}^{2}$=4-$\frac{8}{3}$=$\frac{4}{3}$，
故选：C．
点评 本题考查定积分的运用，解题的关键是确定积分区间与被积函数．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
14．不等式x（x+2）≥0的解集为（ ）
| A． | {x|x≥0或x≤-2} | B． | {x|-2≤x≤0} | C． | {x|0≤x≤2} | D． | {x|x≤0或x≥2} |
18．将分别写有A，B，C，D，E，F的6张卡片装入3个不同的信封里中．若每个信封装2张，其中写有A，B的卡片装入同一信封，则不同的方法共有（ ）
| A． | 12种 | B． | 18种 | C． | 36种 | D． | 54种 |
15．在△ABC中，若A，B，C所对边的长分别为a，b，c，若a=2，B=$\frac{π}{6}$，c=2$\sqrt{3}$，则b=（ ）
| A． | 4 | B． | 2 | C． | 16-4$\sqrt{3}$ | D． | 10 |
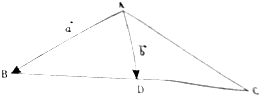如图，在△ABC中，D为BC中点，记$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，已知|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=1，＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=$\frac{π}{3}$．