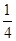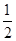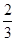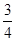题目内容
已知函数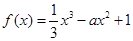
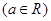 .
.
(Ⅰ)若曲线y=f(x)在(1,f(1))处的切线与直线x+y+1=0平行,求a的值;
(Ⅱ)若a>0,函数y=f(x)在区间(a,a 2-3)上存在极值,求a的取值范围;
(Ⅲ)若a>2,求证:函数y=f(x)在(0,2)上恰有一个零点.
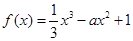
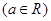 .
.(Ⅰ)若曲线y=f(x)在(1,f(1))处的切线与直线x+y+1=0平行,求a的值;
(Ⅱ)若a>0,函数y=f(x)在区间(a,a 2-3)上存在极值,求a的取值范围;
(Ⅲ)若a>2,求证:函数y=f(x)在(0,2)上恰有一个零点.
(1)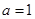 (2)
(2)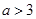
(3)先结合导数分析证明函数f(x)在(0,2)内单调递减.那么得到结论。
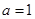 (2)
(2)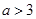
(3)先结合导数分析证明函数f(x)在(0,2)内单调递减.那么得到结论。
试题分析:.解:(Ⅰ)
 , 1分
, 1分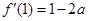 , 2分
, 2分因为曲线y=f(x)在(1,f(1))处的切线与直线x+y+1=0平行
所以
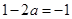 , 3分
, 3分所以
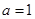 . 4分
. 4分(Ⅱ)令
 , 5分
, 5分即
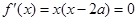 ,所以
,所以 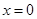 或
或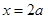 . 6分
. 6分因为a>0,所以
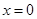 不在区间(a,a2-3)内,
不在区间(a,a2-3)内,要使函数在区间(a,a 2-3)上存在极值,只需
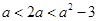 . 7分
. 7分所以
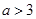 . 9分
. 9分(Ⅲ)证明:令
 ,所以
,所以 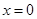 或
或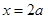 .
.因为a>2,所以2a>4, 10分
所以
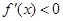 在(0,2)上恒成立,函数f(x)在(0,2)内单调递减.
在(0,2)上恒成立,函数f(x)在(0,2)内单调递减.又因为
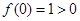 ,
,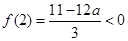 , 11分
, 11分所以f(x)在(0,2)上恰有一个零点. 12分
点评:主要考查了导数在研究函数中的运用,属于基础题。

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
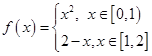 ,则
,则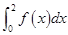 的值为( )
的值为( )



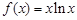 .
. 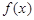 的最小值;
的最小值;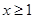 都有
都有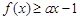 ,求实数
,求实数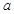 的取值范围.
的取值范围.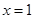 是有极大值4,当
是有极大值4,当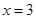 是有极小值0,且函数过原点,则此函数是( )
是有极小值0,且函数过原点,则此函数是( )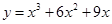
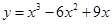
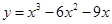
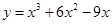
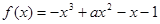 在
在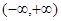 上是单调函数,则实数a的取值范围是( )
上是单调函数,则实数a的取值范围是( )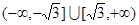
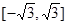
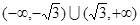
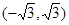
 在点
在点 处的切线与直线
处的切线与直线 平行,则
平行,则 =( )
=( ) ;
;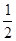 ;
; ;
;
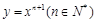 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为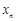 ,令
,令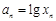 ,则
,则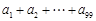 的值为 .
的值为 .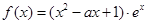 .
.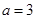 时,求曲线
时,求曲线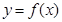 在点
在点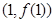 处的切线方程;
处的切线方程;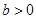 ,
,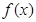 在区间
在区间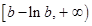 上是增函数,求实数
上是增函数,求实数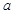 的取值范围.
的取值范围.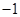 ≤a≤1,
≤a≤1,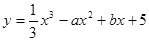 有极值的概率为( )
有极值的概率为( )