题目内容
(本小题满分13分)f(x)为定义在R上的偶函数,但x≥0时,y= f(x)的图像是顶点在P(3,4),且过点A(2,2)的抛物线的一部分。
(1)求函数f(x)在(-∞,0)上的解析式;
(2)求函数f(x)在R上的解析式,并画出函数f(x)的图像;
(3)写出函数f(x)的单调区间
(1)求函数f(x)在(-∞,0)上的解析式;
(2)求函数f(x)在R上的解析式,并画出函数f(x)的图像;
(3)写出函数f(x)的单调区间
见解析。
本试题主要是考查了函数的奇偶性和函数的解析式的求解,以及函数的图像与单调性的综合运用。
(1)因为f(x)为定义在R上的偶函数,但x≥0时,y= f(x)的图像是顶点在P(3,4),且过点A(2,2)的抛物线的一部分,那么设出解析式,然后利用偶函数的对称性得到结论。
(2)将第一问的结论和条件合并得到分段函数的解析式,并作出图像。
(3)根据图像法,得到函数的单调区间。
(1)因为f(x)为定义在R上的偶函数,但x≥0时,y= f(x)的图像是顶点在P(3,4),且过点A(2,2)的抛物线的一部分,那么设出解析式,然后利用偶函数的对称性得到结论。
(2)将第一问的结论和条件合并得到分段函数的解析式,并作出图像。
(3)根据图像法,得到函数的单调区间。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
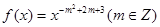 为偶函数,且在区间
为偶函数,且在区间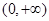 上是单调增函数.则函数
上是单调增函数.则函数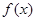 的解析式为 ;
的解析式为 ;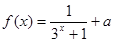 是奇函数,则实数
是奇函数,则实数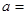
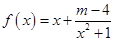 为奇函数,则
为奇函数,则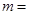 .
.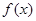 为奇函数,
为奇函数,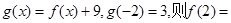 .
.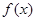 是
是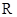 上的奇函数,对
上的奇函数,对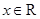 都有
都有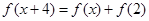 成立,若
成立,若 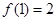 , 则
, 则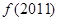 等于( )
等于( )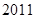
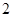
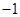
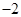
 是定义在R上的函数,且满足
是定义在R上的函数,且满足 ,当
,当 时,
时, ,则
,则 ( )
( )



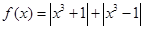 ,则下列坐标表示的点一定在函数f(x)图象上的是( )
,则下列坐标表示的点一定在函数f(x)图象上的是( )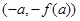
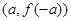
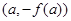
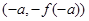
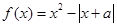 为偶函数,则实数
为偶函数,则实数