题目内容
(本小题满分14分)如图,在平面直角坐标系xOy中,椭圆C的中心在坐标原点O,右焦点为F.若C的右准线l的方程为x=4,离心率e=.
(1)求椭圆C的标准方程;
(2)设点P为直线l上一动点,且 在x轴上方.圆M经过O、F、P三点,求当圆心M到x轴的距离最小时圆M的方程.
在x轴上方.圆M经过O、F、P三点,求当圆心M到x轴的距离最小时圆M的方程.
解:(1)由题意,设椭圆C的标准方程为  则
则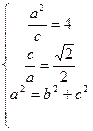 得:
得: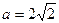 ,
,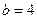 ,
,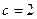
所以所求椭圆C的方程为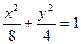
(2)方法一、由(1)知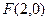 ,由题意可设
,由题意可设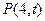
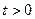
线段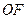 的垂直平分线方程为
的垂直平分线方程为 ①
①
因为线段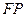 的中心为
的中心为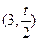 ,斜率为
,斜率为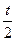 .
.
所以线段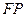 的垂直平分线方程为
的垂直平分线方程为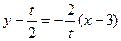
即: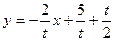 ②
②
联立①②,解得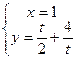
即:圆心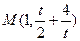
因为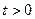 ,所以
,所以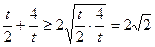 ,当且仅当
,当且仅当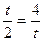 即:
即: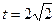 时,
时,
圆心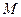 到
到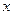 轴的距离最小,此时圆心为
轴的距离最小,此时圆心为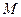
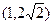 ,半径为
,半径为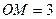 ,
,
故所求圆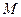 的方程为
的方程为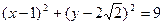 .
.
方法二:由(1)知F(2,0)由题可设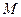 的方程为
的方程为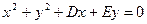
将点F、P的坐标代入得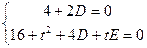 解得:
解得: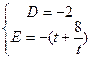
所以圆心的坐标为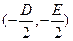 ,即:
,即: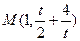

因为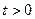 ,所以
,所以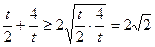 ,当且仅当
,当且仅当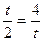 即:
即: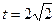 时,
时,
所以圆心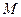 到
到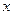 轴的距离最小,此时
轴的距离最小,此时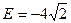
故所求圆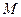 的方程为:
的方程为: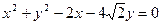
解析

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
极坐标系中,以(9, )为圆心,9为半径的圆的极坐标方程为( )
)为圆心,9为半径的圆的极坐标方程为( )
A.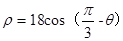 | B.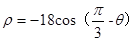 |
C.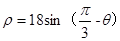 | D.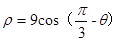 |
若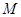 点的极坐标为
点的极坐标为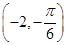 ,则
,则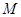 点的直角坐标是( )
点的直角坐标是( )
A.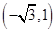 | B.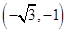 | C. | D.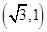 |

 圆
圆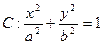 ,
,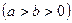 的离心率为
的离心率为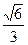 ,直线
,直线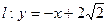 与以
与以 原点为圆心,以椭圆
原点为圆心,以椭圆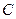 的短半轴长为半径的圆相切。
的短半轴长为半径的圆相切。 、求椭圆
、求椭圆 、过点
、过点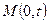 的直线
的直线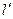 (斜率存在时)与椭圆
(斜率存在时)与椭圆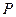 、
、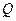 两点,设
两点,设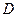 为椭圆
为椭圆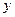 轴负半轴的交点,且
轴负半轴的交点,且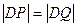 ,求实数
,求实数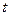 的取值范围。
的取值范围。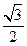 的椭圆
的椭圆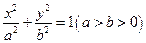 上的点到
上的点到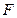 的最长距离为
的最长距离为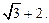
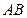 ,若点
,若点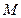 在
在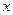 轴上,且使得
轴上,且使得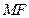 为
为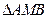 的一条内角平分线,则称点
的一条内角平分线,则称点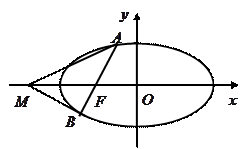
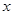 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,已知直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,已知直线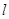 的参数方程是
的参数方程是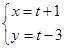 (
(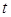 为参数),圆
为参数),圆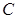 的极坐标方程是
的极坐标方程是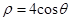 ,则直线
,则直线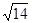
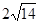
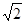
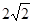
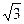 )的直线l过点(0,-2
)的直线l过点(0,-2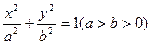
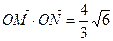 cot∠MON ≠0(O为原点).若存在,求直线m的方程;若不存
cot∠MON ≠0(O为原点).若存在,求直线m的方程;若不存
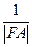 +
+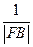 为定值.
为定值.