题目内容
(本题满分15分) 设抛物线C1:x2=4y的焦点为F,曲线C2与C1关于原点对称.
(Ⅰ) 求曲线C2的方程;
(Ⅱ) 曲线C2上是否存在一点P(异于原点),过点P作C1的两条切线PA,PB,切点A,B,满足| AB |是 | FA | 与 | FB | 的等差中项?若存在,求出点P的坐标;若不存在,请说明理由
(Ⅰ)解;因为曲线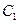 与
与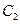 关于原点对称,又
关于原点对称,又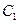 的方程
的方程 ,
,
所以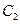 方程为
方程为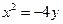 .
.
(Ⅱ)解:设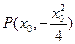 ,
,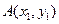 ,
,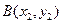 ,
,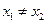 .
. 的导数为
的导数为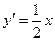 ,则切线
,则切线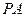 的方程
的方程 ,
,
又 ,得
,得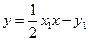 ,
,
因点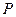 在切线
在切线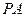 上,故
上,故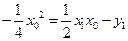 .
.
同理, 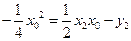 .
.
所以直线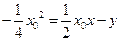 经过
经过 两点,
两点,
即直线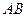 方程为
方程为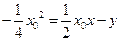 ,即
,即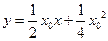 ,
,
代入 得
得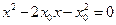 ,则
,则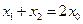 ,
,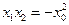 ,
,
所以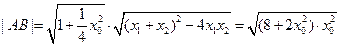 ,
,
由抛物线定义得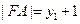 ,
,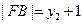 .
.
所以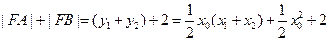 ,
,
由题设知,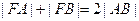 ,即
,即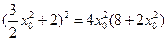 ,
,
解得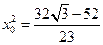 ,从而
,从而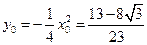 .
.
综上,存在点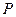 满足题意,点
满足题意,点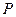 的坐标为
的坐标为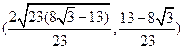 或
或 .
.
解析

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
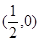 的距离与P到直线
的距离与P到直线 距离相等
距离相等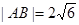 ,求直线l的方程;
,求直线l的方程;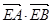 恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.
恒为定值?若存在,求出E的坐标及定值;若不存在,请说明理由.  的左、右焦点分别为
的左、右焦点分别为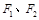 ,上顶点为
,上顶点为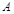 ,离心率为
,离心率为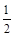 ,在
,在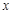 轴负半轴上有一点
轴负半轴上有一点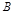 ,且
,且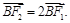
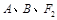 三点的圆恰好与直线
三点的圆恰好与直线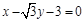 相切,求椭圆C的方程;
相切,求椭圆C的方程;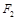 作斜率为
作斜率为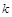 的直线
的直线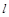 与椭圆C交于
与椭圆C交于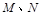 两点,在
两点,在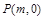 ,使得以
,使得以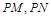 为邻边的平行四边形是菱形?如果存在,求出
为邻边的平行四边形是菱形?如果存在,求出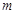 的取值范围;否则,请说明理由.
的取值范围;否则,请说明理由.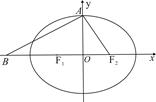
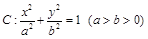 的左、右焦点分别为
的左、右焦点分别为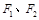 ,上顶点为
,上顶点为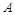 ,离心率为
,离心率为 ,在
,在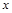 轴负半轴上有一点
轴负半轴上有一点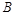 ,且
,且
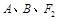 三点的圆恰好与直线
三点的圆恰好与直线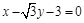 相切,求椭圆C的方程;
相切,求椭圆C的方程;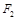 作斜率为
作斜率为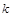 的直线
的直线 与椭圆C交于
与椭圆C交于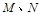 两点,在
两点,在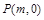 ,使得以
,使得以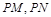 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出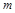 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.
 与抛物线
与抛物线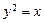 交于
交于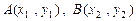 两点,与
两点,与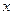 轴相交于点
轴相交于点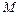 ,且
,且 .
.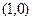 ;
;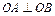 ;
;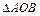 的面积的最小值.
的面积的最小值.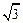 ,求△AOB面积的最大值.
,求△AOB面积的最大值.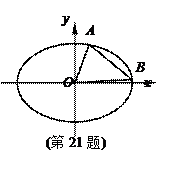

 在x轴上方.圆M经过O、F、P三点,求当圆心M到x轴的距离最小时圆M的方程.
在x轴上方.圆M经过O、F、P三点,求当圆心M到x轴的距离最小时圆M的方程.
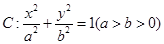 的长轴长是短轴长的两倍,且过点
的长轴长是短轴长的两倍,且过点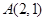
 的标准方程;
的标准方程;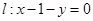 与椭圆
与椭圆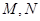 ,求
,求 的值.
的值. 过椭圆
过椭圆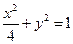 的右焦点,交椭圆于
的右焦点,交椭圆于 两点,求
两点,求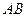 长
长