题目内容
(本小题满分12分)
已知方向向量为v=(1,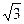 )的直线l过点(0,-2
)的直线l过点(0,-2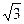 )和椭圆C:
)和椭圆C: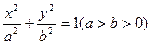
的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
(Ⅰ)求椭圆C的方程;(Ⅱ)是否存在过点E(-2,0)的直线m交椭圆C于点M、N,满足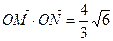 cot∠MON ≠0(O为原点).若存在,求直线m的方程;若不存
cot∠MON ≠0(O为原点).若存在,求直线m的方程;若不存
在,请说明理由.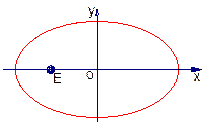
(I)解法一:直线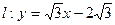 , ①
, ①
过原点垂直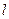 的直线方程为
的直线方程为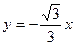 , ②
, ②
解①②得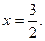
∵椭圆中心(0,0)关于直线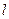 的对称点在椭圆C的右准线上,
的对称点在椭圆C的右准线上,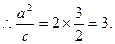
∵直线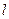 过椭圆焦点,∴该焦点坐标为(2,0).
过椭圆焦点,∴该焦点坐标为(2,0).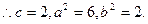 故椭圆C的方程为
故椭圆C的方程为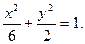 ③
③
解法二:直线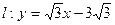 .
.
设原点关于直线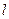 对称点为(p,q),则
对称点为(p,q),则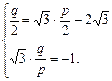 解得p=3.
解得p=3.
∵椭圆中心(0,0)关于直线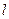 的对称点在椭圆C的右准线上,
的对称点在椭圆C的右准线上,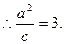 ∵直线
∵直线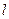 过椭圆焦点,∴该焦点坐标为(2,0).
过椭圆焦点,∴该焦点坐标为(2,0).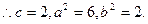 故椭圆C的方程为
故椭圆C的方程为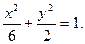 ③
③
(II)解法一:设M(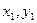 ),N(
),N(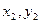 ).
).
当直线m不垂直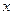 轴时,直线
轴时,直线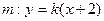 代入③,整理得
代入③,整理得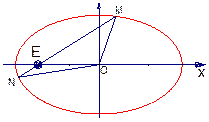
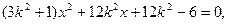
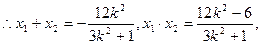
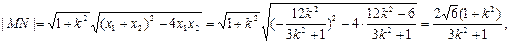
点O到直线MN的距离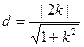
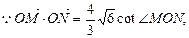 即
即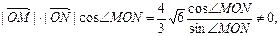
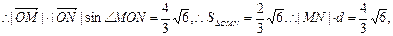
即
整理得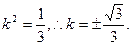
当直线m垂直x轴时,也满足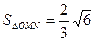 .
.
故直线m的方程为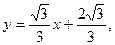
或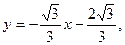 或
或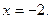
经检验上述直线均满足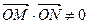 .
.
所以所求直线方程为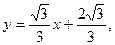 或
或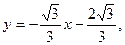 或
或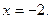
解法二:设M(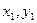 ),N(
),N(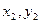 ).
).
当直线m不垂直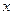 轴时,直线
轴时,直线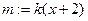 代入③,整理得
代入③,整理得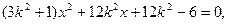
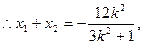
∵E(-2,0)是椭圆C的左焦点,
∴|MN|=|ME|+|NE|
=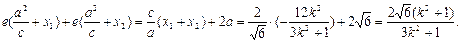
以下与解法一相同.
解法三:设M(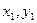 ),N(
),N(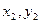 ).
).
设直线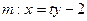 ,代入③,整理得
,代入③,整理得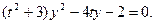
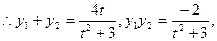
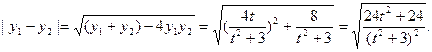
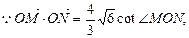
即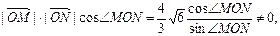
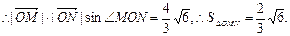
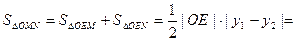
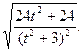
∴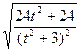 =
=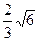 ,整理得
,整理得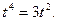
解得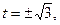 或
或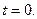
故直线m的方程为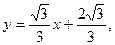 或
或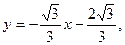 或
或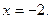
经检验上述直线方程为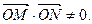
所以所求直线方程为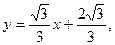 或
或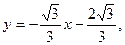 或
或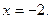 解析
解析

练习册系列答案
相关题目
极坐标系中,由三条曲线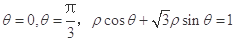 围成的图形的面积是( )
围成的图形的面积是( )
A.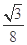 | B.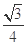 | C.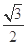 | D. |
在极坐标系中与圆 相切的一条直线的方程为( )
相切的一条直线的方程为( )
A. | B.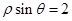 |
C. | D. |
若直线的参数方程为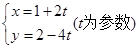 ,则直线的斜率为( )
,则直线的斜率为( )
A.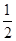 | B. | C. | D. |
在极坐标系中,圆ρ=-2sinθ的圆心的极坐标是( )
A.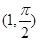 | B.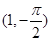 | C.(1,0) | D.(1,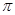 ) ) |
 与抛物线
与抛物线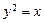 交于
交于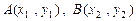 两点,与
两点,与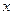 轴相交于点
轴相交于点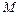 ,且
,且 .
.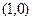 ;
;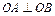 ;
;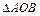 的面积的最小值.
的面积的最小值. 1,y1),C(x2,y2)满足条件|F2A|,|F2B|,|F2C|成等差数列.(1)求该椭圆的方程;(2)求弦AC中点的横坐标.
1,y1),C(x2,y2)满足条件|F2A|,|F2B|,|F2C|成等差数列.(1)求该椭圆的方程;(2)求弦AC中点的横坐标. =1(a>b>0)的离心率为
=1(a>b>0)的离心率为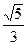 ,短轴一
,短轴一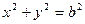 的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.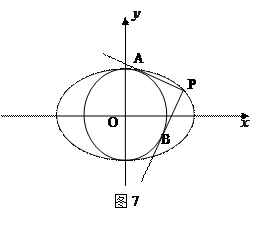

 在x轴上方.圆M经过O、F、P三点,求当圆心M到x轴的距离最小时圆M的方程.
在x轴上方.圆M经过O、F、P三点,求当圆心M到x轴的距离最小时圆M的方程.