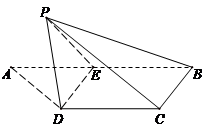题目内容
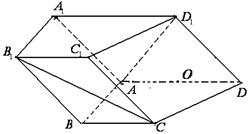
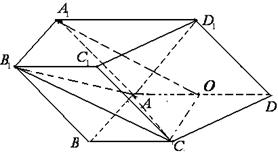
如图,在四棱柱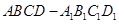 中,侧面
中,侧面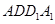 ⊥底面
⊥底面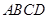 ,
,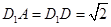 ,底面
,底面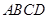 为直角梯形,其中
为直角梯形,其中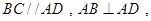
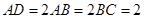 ,O为
,O为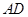 中点。
中点。
(Ⅰ)求证: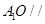 平面
平面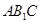 ;
;
(Ⅱ)求锐二面角A—C1D1—C的余弦值。
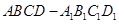 中,侧面
中,侧面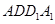 ⊥底面
⊥底面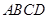 ,
,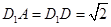 ,底面
,底面 为直角梯形,其中
为直角梯形,其中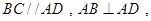
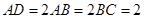 ,O为
,O为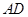 中点。
中点。(Ⅰ)求证:
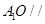 平面
平面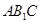 ;
;(Ⅱ)求锐二面角A—C1D1—C的余弦值。

(Ⅰ)证明:如图,连接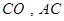 , …………..1分
, …………..1分
则四边形 为正方形, …………..2分
为正方形, …………..2分
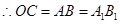 ,且
,且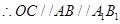
故四边形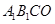 为平行四边形,…………..3分
为平行四边形,…………..3分
 , …………..4分
, …………..4分
又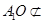 平面
平面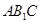 ,
,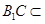 平面
平面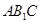 ……..5分
……..5分
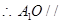 平面
平面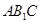 …………..6分
…………..6分
(Ⅱ) 为
为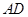 的中点,
的中点, ,又侧面
,又侧面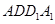 ⊥底面
⊥底面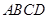 ,故
,故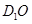 ⊥底面
⊥底面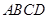 ,…………..7分
,…………..7分
以 为原点,所
为原点,所 在直线分别为
在直线分别为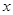 轴,
轴,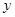 轴,
轴,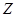 轴建立如图所示的坐标系,则
轴建立如图所示的坐标系,则
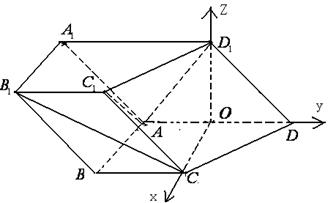
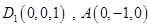 ,…………..8分
,…………..8分
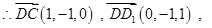
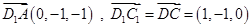 ,…………..9分
,…………..9分
设 为平面
为平面 的一个法向量,由
的一个法向量,由 ,得
,得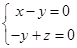 ,
,
令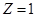 ,则
,则 ………..10分
………..10分
又设 为平面
为平面 的一个法向量,由
的一个法向量,由 ,得
,得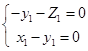 ,令
,令
 ,则
,则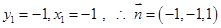 ,………..11分
,………..11分
则 ,故所求锐二面角A—C1D1—C的余弦值为
,故所求锐二面角A—C1D1—C的余弦值为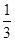
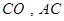 , …………..1分
, …………..1分则四边形
 为正方形, …………..2分
为正方形, …………..2分
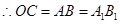 ,且
,且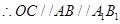
故四边形
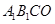 为平行四边形,…………..3分
为平行四边形,…………..3分 , …………..4分
, …………..4分又
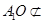 平面
平面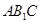 ,
,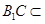 平面
平面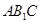 ……..5分
……..5分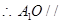 平面
平面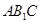 …………..6分
…………..6分(Ⅱ)
 为
为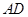 的中点,
的中点, ,又侧面
,又侧面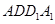 ⊥底面
⊥底面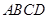 ,故
,故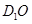 ⊥底面
⊥底面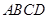 ,…………..7分
,…………..7分以
 为原点,所
为原点,所 在直线分别为
在直线分别为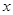 轴,
轴,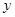 轴,
轴,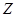 轴建立如图所示的坐标系,则
轴建立如图所示的坐标系,则

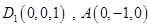 ,…………..8分
,…………..8分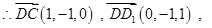
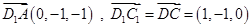 ,…………..9分
,…………..9分设
 为平面
为平面 的一个法向量,由
的一个法向量,由 ,得
,得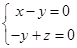 ,
,令
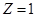 ,则
,则 ………..10分
………..10分又设
 为平面
为平面 的一个法向量,由
的一个法向量,由 ,得
,得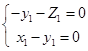 ,令
,令 ,则
,则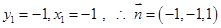 ,………..11分
,………..11分则
 ,故所求锐二面角A—C1D1—C的余弦值为
,故所求锐二面角A—C1D1—C的余弦值为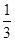
略

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
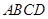 是矩形,
是矩形,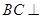 平面
平面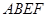 ,四边形
,四边形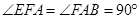 ,
,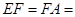
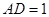 ,点
,点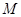 是
是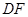 的中点,
的中点,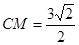 .
.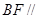 平面
平面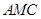 ;
;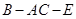 的余弦值.
的余弦值. 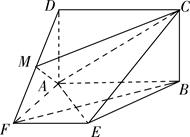
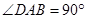 ,
,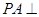 平面ABCD,PA=AB=BC=3,梯形上底AD=1。
平面ABCD,PA=AB=BC=3,梯形上底AD=1。 平面PAB;
平面PAB;
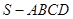 中,
中,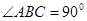 ,
,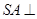 面
面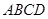 ,
, ,
,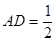 。
。 ;
;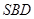 的距离。
的距离。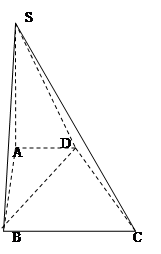
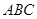 —
—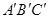 中,点D是BC的中点,欲过点
中,点D是BC的中点,欲过点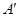 作一截面与平面
作一截面与平面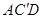 平行,问应当怎样画线,并说明理由。
平行,问应当怎样画线,并说明理由。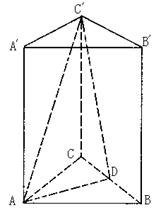
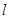 上有无数点不在平面
上有无数点不在平面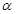 内,则
内,则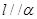
 中,已知
中,已知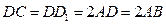 ,
,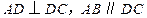 .
.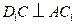 ;
;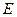 是
是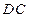 上一点,试确定
上一点,试确定 平面
平面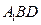 ,并证明.
,并证明.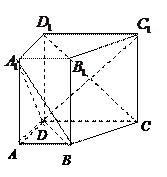
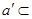 平面
平面 ,直线
,直线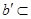 平面
平面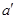 ∥
∥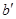 ,其中
,其中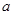 和直线
和直线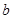 在平面
在平面 AB=a,E是AB的中点,将ΔADE沿DE折起,使点A折到点P的位置,且二面角P-DE-C的大小为120°.
AB=a,E是AB的中点,将ΔADE沿DE折起,使点A折到点P的位置,且二面角P-DE-C的大小为120°.