题目内容
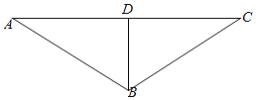
【题目】如图,某运动员从A市出发沿海岸一条笔直公路以每小时15km的速度向东进行长跑训练,长跑开始时,在A市南偏东方向距A市75km,且与海岸距离为45km的海上B处有一艘划艇与运动员同时出发,要追上这位运动员.

(1)划艇至少以多大的速度行驶才能追上这位运动员?
(2)求划艇以最小速度行驶时的行驶方向与![]() 所成的角.
所成的角.
(3)若划艇每小时最快行驶11.25km,划艇全速行驶,应沿何种路线行驶才能尽快追上这名运动员,最快需多长时间?
【答案】(1)9![]() ;(2)
;(2)![]() ;(3)划艇应垂直于海岸向北的方向行驶才能尽快追上这名运动员;
;(3)划艇应垂直于海岸向北的方向行驶才能尽快追上这名运动员;![]() .
.
【解析】
(1)设速度为![]() ,时间为
,时间为![]() ,由余弦定理可得
,由余弦定理可得![]() 关于时间
关于时间![]() 的函数,根据二次函数的性质得出
的函数,根据二次函数的性质得出![]() 的最小值;
的最小值;
(2)利用余弦定理计算![]() 即可得出答案.
即可得出答案.
(3)假设划艇沿着垂直于海岸的方向,即![]() 方向行驶需要
方向行驶需要![]() ,而
,而![]() 运动员刚好到点
运动员刚好到点![]() ,即可得出结果.
,即可得出结果.
(1)设划艇以![]()
![]() 的速度从
的速度从![]() 处出发,沿
处出发,沿![]() 方向,
方向,![]()
![]() 后与运动员在
后与运动员在![]() 处相遇,
处相遇,
过![]() 作
作![]() 的垂线
的垂线![]() ,则
,则![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() .
.
由余弦定理,得![]() ,
,
得![]() .
.
整理得:![]()
![]() .
.
当![]() ,即
,即![]() 时,
时,![]() 取得最小值81,即
取得最小值81,即![]() ,
,
所以划艇至少以9![]() 的速度行驶才能把追上这位运动员.
的速度行驶才能把追上这位运动员.
(2)当![]()
![]() 时,
时,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由余弦定理,得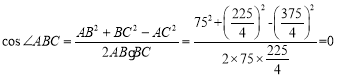 ,
,
所以![]() ,
,
所以划艇以最小速度行驶时的行驶方向与![]() 所成的角为
所成的角为![]() .
.
(3)划艇每小时最快行驶11.25km全速行驶,
假设划艇沿着垂直于海岸的方向,即![]() 方向行驶,而
方向行驶,而![]() ,
,
此时到海岸距离最短,需要的时间最少,
所以需要:![]() ,而
,而![]() 时运动员向东跑了:
时运动员向东跑了:![]() ,
,
而![]() ,即
,即![]() 时,划艇和运动员相遇在点
时,划艇和运动员相遇在点![]() .
.
所以划艇应垂直于海岸向北的方向行驶才能尽快追上这名运动员,最快需要![]() .
.

【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如下:

(1)根据箱产量的频率分布直方图填写下面![]() 列联表,从等高条形图中判断箱产量是否与新、旧网箱养殖方法有关;
列联表,从等高条形图中判断箱产量是否与新、旧网箱养殖方法有关;
(2)根据列联表判断是否有99%的把握认为箱产量与养殖方法有关?
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
参考公式:
(1)给定临界值表
P(K | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)![]() 其中
其中![]() 为样本容量.
为样本容量.
【题目】近年电子商务蓬勃发展, ![]() 年某网购平台“双
年某网购平台“双![]() ”一天的销售业绩高达
”一天的销售业绩高达![]() 亿元人民币,平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出
亿元人民币,平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出![]() 次成功交易,并对其评价进行统计,网购者对商品的满意率为
次成功交易,并对其评价进行统计,网购者对商品的满意率为![]() ,对快递的满意率为
,对快递的满意率为![]() ,其中对商品和快递都满意的交易为
,其中对商品和快递都满意的交易为![]() 次.
次.
(1)根据已知条件完成下面的![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为“网购者对商品满意与对快递满意之间有关系”?
的把握认为“网购者对商品满意与对快递满意之间有关系”?
对快递满意 | 对快递不满意 | 合计 | |
对商品满意 |
| ||
对商品不满意 | |||
合计 |
|
(2)若将频率视为概率,某人在该网购平台上进行的![]() 次购物中,设对商品和快递都满意的次数为随机变量
次购物中,设对商品和快递都满意的次数为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
附:  (其中
(其中![]() 为样本容量)
为样本容量)
|
|
|
|
|
|
|
|
|
|
|
|

