Question

【题目】已知函数 ，x R其中a>0.

（Ⅰ）求函数f(x)的单调区间；

（Ⅱ）若函数f(x)在区间(-3,0)内恰有两个零点，求a的取值范围；

（Ⅲ）当a=1时，设函数f(x)在区间[t,t+3]上的最大值为M(t)，最小值为m(t),记 ,求函数g(t)在区间[-4,-1]上的最小值.

Answer 1

【答案】(1)增区间：和；减区间：；(2)；(3).

【解析】

试题（1）先求出函数的导函数，由，得出函数的极值点，进而列出表格，写出函数的单调增、减区间即可；（2）结合（1）中所求，得出判断：在内单调递增，在内单调递减，进而得出函数在内恰有两个零点的条件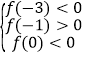，从中求解即可得出的取值范围；（3）根据及（1）中的结果，作出判断在内单调递增，在内单调递减，在内单调递增，然后分、、三种情况进行确定函数的最大值与最小值，进而确定在各段的最小值，最后比较这三段的最小值，即可得出所求的最小值.

试题解析：（1）1分

时，或

		0		0

函数单调增区间为，；减区间为4分

（2）由（1）知在内单调递增，在内单调递减

所以函数在内恰有两个零点当且仅当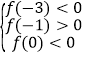

解得，的取值范围是8分

（3），由（1）知：在内单调递增，在内单调递减，在内单调递增

①当

②，在单调递增，在单调递减..最小值是与的较小者

，

，在递减，最小值为

①②可以合并11分

③，

最大值为与较大者，最小值为与较小者

在，上单调递增

而

，，

综上，函数在上的最小值为13分.