题目内容
(本小题满分12分)已知直线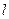 过定点
过定点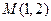 ,且与抛物线
,且与抛物线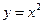 交于
交于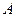 、
、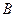 两点,抛物线在
两点,抛物线在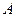 、
、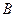 两点处的切线的相交于点
两点处的切线的相交于点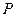 .
.
(I)求点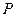 的轨迹方程;
的轨迹方程;
(II)求三角形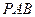 面积的最小值.
面积的最小值.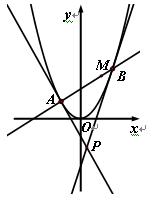
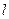 过定点
过定点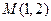 ,且与抛物线
,且与抛物线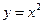 交于
交于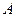 、
、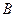 两点,抛物线在
两点,抛物线在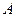 、
、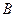 两点处的切线的相交于点
两点处的切线的相交于点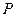 .
.(I)求点
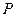 的轨迹方程;
的轨迹方程;(II)求三角形
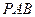 面积的最小值.
面积的最小值.
(1)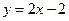 (2)2
(2)2
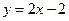 (2)2
(2)2(Ⅰ)设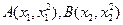 ,
,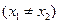 ,
,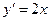
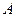 处的切线方程为
处的切线方程为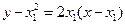 整理得
整理得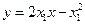 ,①
,①
同理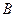 处的切线方程为
处的切线方程为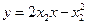 ② …………………………………2分
② …………………………………2分
联立①②得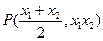 …………………………………3分
…………………………………3分
由题意知直线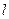 的斜率存在,设斜率为
的斜率存在,设斜率为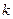 ,
,
则直线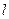 的方程为:
的方程为: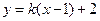 ③,
③,
③与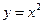 联立得
联立得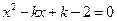
 , …………………………………5分
, …………………………………5分
得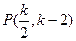 , ………………………………6分
, ………………………………6分
即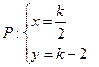 所以
所以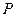 的轨迹方程为:
的轨迹方程为: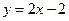 ………………………7分
………………………7分
(Ⅱ)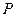 到直线
到直线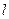 的距离
的距离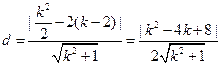

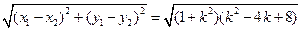
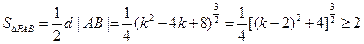 ……………………12分
……………………12分
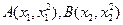 ,
,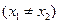 ,
,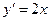
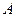 处的切线方程为
处的切线方程为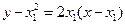 整理得
整理得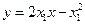 ,①
,①同理
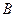 处的切线方程为
处的切线方程为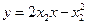 ② …………………………………2分
② …………………………………2分联立①②得
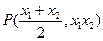 …………………………………3分
…………………………………3分由题意知直线
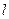 的斜率存在,设斜率为
的斜率存在,设斜率为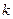 ,
,则直线
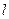 的方程为:
的方程为: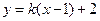 ③,
③,③与
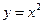 联立得
联立得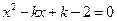
 , …………………………………5分
, …………………………………5分得
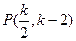 , ………………………………6分
, ………………………………6分即
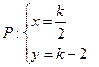 所以
所以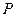 的轨迹方程为:
的轨迹方程为: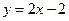 ………………………7分
………………………7分(Ⅱ)
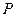 到直线
到直线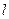 的距离
的距离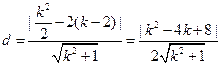

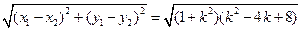
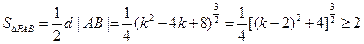 ……………………12分
……………………12分
练习册系列答案
相关题目
 已知抛物线
已知抛物线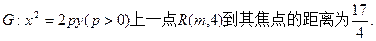
 为—1的直线l交抛物线G于另一点A,交x轴于点B,若|OA|=|OB|(O为坐标原点),求点P的坐标。
为—1的直线l交抛物线G于另一点A,交x轴于点B,若|OA|=|OB|(O为坐标原点),求点P的坐标。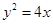 上的两点A、B满足
上的两点A、B满足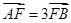 ,则弦AB的中点到准线的距离为___________.
,则弦AB的中点到准线的距离为___________.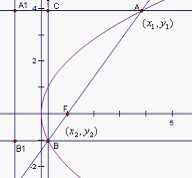
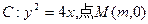 在x轴的正半轴上,过M的直线
在x轴的正半轴上,过M的直线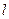 与C相交于A、B两点,O为坐标原点。
与C相交于A、B两点,O为坐标原点。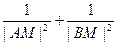 恒为定值。
恒为定值。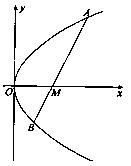
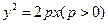 的焦点与椭圆
的焦点与椭圆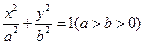 的一个焦点重合,且抛物线与椭圆的一个交点为
的一个焦点重合,且抛物线与椭圆的一个交点为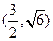 ,(1)求抛物线与椭圆的方程,(2)若过点
,(1)求抛物线与椭圆的方程,(2)若过点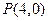 的直线与抛物线交于点
的直线与抛物线交于点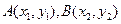 ,求
,求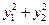 的最小值
的最小值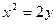
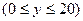 ,在杯中放入一个球,要使球触及酒杯的底部,则球的半径
,在杯中放入一个球,要使球触及酒杯的底部,则球的半径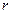 的取值范围是 。
的取值范围是 。 ),一辆卡车空车时能通过此隧道,现载一集装箱,箱宽3
),一辆卡车空车时能通过此隧道,现载一集装箱,箱宽3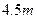 ,此车是否能通过隧道?并说明理由.
,此车是否能通过隧道?并说明理由.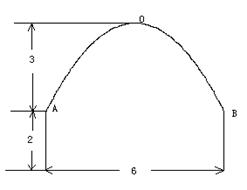
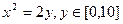 ,在杯内放入一个清洁球,要求清洁球能擦净酒杯的最底部(如图),则清洁球的最大半径为
,在杯内放入一个清洁球,要求清洁球能擦净酒杯的最底部(如图),则清洁球的最大半径为 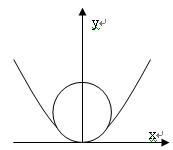
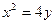 的焦点为F,准线与y轴的交点为M,N为抛物线上的一点,且
的焦点为F,准线与y轴的交点为M,N为抛物线上的一点,且 。
。