题目内容
16．已知f（x）=|1-2x|，x∈[0，1]，那么方程f（f（f（x）））=x的解的个数是8．分析 作函数y=f（f（f（x）））与函数y=x的图象，从而化方程f（f（f（x）））=x的解的个数为函数图象交点的个数，从而数形结合求得．
解答 解：作函数y=f（f（f（x）））与函数y=x的图象如下，
结合图象可知，
方程f（f（f（x）））=x的解的个数是8；
故答案为：8．
点评 本题考查了数形结合的应用及函数图象与方程的根的关系应用，属于中档题．
练习册系列答案
相关题目
6．
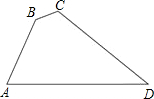如图，在四边形ABCD中，∠B=135°，∠C=120°，AB=2$\sqrt{3}$，BC=4-2$\sqrt{2}$，CD=4$\sqrt{2}$，则AD边的长为（ ）
如图，在四边形ABCD中，∠B=135°，∠C=120°，AB=2$\sqrt{3}$，BC=4-2$\sqrt{2}$，CD=4$\sqrt{2}$，则AD边的长为（ ）| A． | 2$\sqrt{6}$ | B． | 4$\sqrt{6}$ | C． | 4+$\sqrt{6}$ | D． | 2+2$\sqrt{6}$ |
5．如果方程x2+$\frac{{y}^{2}}{k}$=2表示焦点在x轴上的椭圆，那么实数k的取值范围是（ ）
| A． | （0，2） | B． | （1，+∞） | C． | （0，1） | D． | （1，2） |
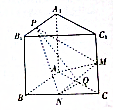如图，已知有直三棱柱ABC-A1B1C1中，AA1=AB=AC=1，AB⊥AC，M、N、Q分别是CC1、BC、AC的中点，点P在线段A1B1上运动．