题目内容
18.已知数列{an}{bn},对任何正整数n,都有a1b1+a2b2+a3b3+…+an-1•bn-1+an•bn=(n-1)•2n+1(1)若数列{bn}是首项为1,公比为2的等比数列,求数列{an}通项公式;
(2)求证:$\frac{1}{{a}_{1}•{b}_{1}}$+$\frac{1}{{a}_{2}•{b}_{2}}$+$\frac{1}{{a}_{3}•{b}_{3}}$+…+$\frac{1}{{a}_{n}•{b}_{n}}$<$\frac{3}{2}$.
分析 (1)仿写等式,两式相减得到anbn=n•2(n-1)利用等比数列的通项公式求出bn=2(n-1)代入求出an=n;
(2)由$\frac{1}{{a}_{i}{b}_{i}}$=$\frac{1}{i•{2}^{i-1}}$,通过放缩法得到要证的不等式.
解答 解:(1)由题意可得n=1时,a1b1=1,
a1b1+a2b2+a3b3+…+an-1•bn-1+an•bn=(n-1)•2n+1①
将n换为n-1,(n>1),可得a1b1+a2b2+a3b3+…+an-1•bn-1=(n-2)•2n-1+1②
①-②,可得anbn=(n-1)•2n-(n-2)•2n-1=n•2n-1,
由首项为1,公比为2的等比数列,可得bn=2n-1,
可得an=n;
(2)证明:aibi=i•2(i-1) 所以$\frac{1}{{a}_{i}{b}_{i}}$=$\frac{1}{i•{2}^{i-1}}$,
所以$\sum_{i=1}^{n}$$\frac{1}{{a}_{i}{b}_{i}}$=$\frac{1}{1×{2}^{0}}$+$\frac{1}{2×{2}^{1}}$+$\frac{1}{3×{2}^{2}}$+…+$\frac{1}{n•{2}^{n-1}}$<1+$\frac{1}{4}$+$\frac{1}{8}$+…+$\frac{1}{{2}^{n-1}}$<1+$\frac{\frac{1}{4}-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$
=1+$\frac{1}{2}$-$\frac{1}{{2}^{n-1}}$<$\frac{3}{2}$得证.
点评 求数列的前n项和关键是求出数列的通项,根据通项的特点选择合适的求和方法,考查放缩法的证明不等式.

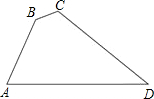 如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=2$\sqrt{3}$,BC=4-2$\sqrt{2}$,CD=4$\sqrt{2}$,则AD边的长为( )
如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=2$\sqrt{3}$,BC=4-2$\sqrt{2}$,CD=4$\sqrt{2}$,则AD边的长为( )| A. | 2$\sqrt{6}$ | B. | 4$\sqrt{6}$ | C. | 4+$\sqrt{6}$ | D. | 2+2$\sqrt{6}$ |