题目内容
15.已知函数f(x)=cos4x-2sinxcosx-sin4x.(Ⅰ)当x∈[0,$\frac{π}{2}$]时,求函数f(x)的值域;
(Ⅱ)若函数g(x)=f(x+$\frac{π}{6}$),求使g(θ)≤-1成立的θ的集合.
分析 (Ⅰ)由三角函数中的恒等变换应用化简函数解析式可得f(x)=$\sqrt{2}$cos(2x+$\frac{π}{4}$),由x∈[0,$\frac{π}{2}$]时,可得2x+$\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{5π}{4}$],从而可求值域.
(Ⅱ)由g(θ)=f(θ+$\frac{π}{6}$)=$\sqrt{2}$cos(2θ+$\frac{7π}{12}$)≤-1,可得cos(2θ+$\frac{7π}{12}$)≤-$\frac{\sqrt{2}}{2}$,由2kπ+$\frac{3π}{4}$≤2θ+$\frac{7π}{12}$≤2kπ+$\frac{5π}{4}$,k∈Z,解得使g(θ)≤-1成立的θ的集合.
解答 解:(Ⅰ)∵f(x)=cos4x-2sinxcosx-sin4x
=(cos2x+sin2x)(cos2x-sin2x)-sin2x=cos2x-sin2x
=$\sqrt{2}$($\frac{\sqrt{2}}{2}$cos2x-$\frac{\sqrt{2}}{2}$sin2x)
=$\sqrt{2}$cos(2x+$\frac{π}{4}$),
∴当x∈[0,$\frac{π}{2}$]时,2x+$\frac{π}{4}$∈[$\frac{π}{4}$,$\frac{5π}{4}$],cos(2x+$\frac{π}{4}$)∈[-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$],f(x)=$\sqrt{2}$cos(2x+$\frac{π}{4}$)∈[-1,1].
(Ⅱ)∵g(θ)=f(θ+$\frac{π}{6}$)=$\sqrt{2}$cos[2(θ+$\frac{π}{6}$)+$\frac{π}{4}$]=$\sqrt{2}$cos(2θ+$\frac{7π}{12}$)≤-1,
∴cos(2θ+$\frac{7π}{12}$)≤-$\frac{\sqrt{2}}{2}$.
∴可得:2kπ+$\frac{3π}{4}$≤2θ+$\frac{7π}{12}$≤2kπ+$\frac{5π}{4}$,k∈Z,解得使g(θ)≤-1成立的θ的集合为:{θ|k$π+\frac{π}{12}$≤θ≤kπ+$\frac{π}{3}$,k∈Z}.
点评 本题主要考查了三角函数中的恒等变换应用,三角函数的图象与性质,属于基本知识的考查.

| A. | $\frac{4}{5}$ | B. | $\frac{8}{5}$ | C. | 1 | D. | $\frac{29}{15}$ |
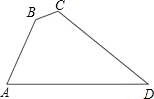 如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=2$\sqrt{3}$,BC=4-2$\sqrt{2}$,CD=4$\sqrt{2}$,则AD边的长为( )
如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=2$\sqrt{3}$,BC=4-2$\sqrt{2}$,CD=4$\sqrt{2}$,则AD边的长为( )| A. | 2$\sqrt{6}$ | B. | 4$\sqrt{6}$ | C. | 4+$\sqrt{6}$ | D. | 2+2$\sqrt{6}$ |
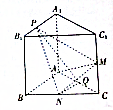 如图,已知有直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,M、N、Q分别是CC1、BC、AC的中点,点P在线段A1B1上运动.
如图,已知有直三棱柱ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,M、N、Q分别是CC1、BC、AC的中点,点P在线段A1B1上运动.