题目内容
14.如图,点F在△OCD所在的区域内(含边界)运动,$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{AC}$=$\frac{1}{3}\overrightarrow{AD}$,且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,当x=-$\frac{1}{3}$时,则y的取值范围是[$\frac{1}{2}$,$\frac{2}{3}$].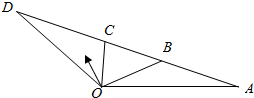
分析 设$\overrightarrow{OE}$=-$\frac{1}{3}$$\overrightarrow{OA}$,过E作EH∥OB,交OD于F,OC于G,BD于H,由$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{AC}$=$\frac{1}{3}\overrightarrow{AD}$,可得B为AC的中点,为AD的三等分点,
可得符合要求的P点位于线段FG上.运用平行线分线段成比例,即可得到所求范围.
解答 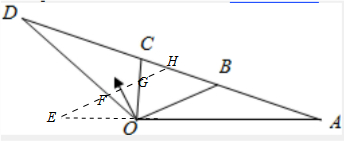 解:设$\overrightarrow{OE}$=-$\frac{1}{3}$$\overrightarrow{OA}$,过E作EH∥OB,
解:设$\overrightarrow{OE}$=-$\frac{1}{3}$$\overrightarrow{OA}$,过E作EH∥OB,
交OD于F,OC于G,BD于H,
由$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{AC}$=$\frac{1}{3}\overrightarrow{AD}$,可得B为AC的中点,
为AD的三等分点,
可得符合要求的P点位于线段FG上.
由平行线分线段成比例,可得
EH=$\frac{4}{3}$OB,FH=$\frac{5}{6}$OB,GH=$\frac{2}{3}$$\overrightarrow{OB}$,
即有EF=$\frac{1}{2}$$\overrightarrow{OB}$,EG=$\frac{2}{3}$OB,
则y的取值范围是[$\frac{1}{2}$,$\frac{2}{3}$].
故答案为:[$\frac{1}{2}$,$\frac{2}{3}$].
点评 本题考查向量的三角形法则,是一个中档题,向量是数形结合的最好的工具,在解题时注意发挥向量的优点.

练习册系列答案
相关题目
5.若$\frac{sinα}{1+cosα}$=$\frac{1}{2}$,则sinα的值为( )
| A. | $\frac{4}{5}$ | B. | $\frac{8}{5}$ | C. | 1 | D. | $\frac{29}{15}$ |
6.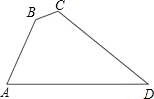 如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=2$\sqrt{3}$,BC=4-2$\sqrt{2}$,CD=4$\sqrt{2}$,则AD边的长为( )
如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=2$\sqrt{3}$,BC=4-2$\sqrt{2}$,CD=4$\sqrt{2}$,则AD边的长为( )
 如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=2$\sqrt{3}$,BC=4-2$\sqrt{2}$,CD=4$\sqrt{2}$,则AD边的长为( )
如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=2$\sqrt{3}$,BC=4-2$\sqrt{2}$,CD=4$\sqrt{2}$,则AD边的长为( )| A. | 2$\sqrt{6}$ | B. | 4$\sqrt{6}$ | C. | 4+$\sqrt{6}$ | D. | 2+2$\sqrt{6}$ |