题目内容
(12分)数列{an}满足a1=1,a2=2,an+2=(1+cos2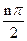 )an+sin
)an+sin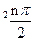 ,n=1、2、3…1)求a3、a4并求数列{an}的通项公式(2)设bn=
,n=1、2、3…1)求a3、a4并求数列{an}的通项公式(2)设bn=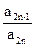 ,令 Sn=
,令 Sn=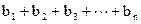 求Sn
求Sn
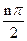 )an+sin
)an+sin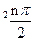 ,n=1、2、3…1)求a3、a4并求数列{an}的通项公式(2)设bn=
,n=1、2、3…1)求a3、a4并求数列{an}的通项公式(2)设bn=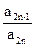 ,令 Sn=
,令 Sn=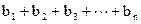 求Sn
求Sn(1) an=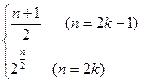 (2) Sn=2-
(2) Sn=2-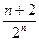
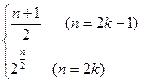 (2) Sn=2-
(2) Sn=2-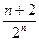
:(1)a3="2 " a4="4 " 当n=2k-1时,a2k+1=a2k-1+1
∴a1,a3,a5…a2k-1…成等差数列,公差d=1
a2k-1=1+(k-1)·1=k∴an= 当n=2k时 a2k+2=2·a2k
当n=2k时 a2k+2=2·a2k
即数列a2,a4,a6…成等比数列,公比q=2a2k=2·2k-1=2k∴an=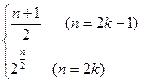
(2)bn=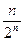 Sn=1
Sn=1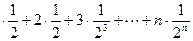 由错位相减得:Sn=2-
由错位相减得:Sn=2-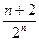
∴a1,a3,a5…a2k-1…成等差数列,公差d=1
a2k-1=1+(k-1)·1=k∴an=
 当n=2k时 a2k+2=2·a2k
当n=2k时 a2k+2=2·a2k即数列a2,a4,a6…成等比数列,公比q=2a2k=2·2k-1=2k∴an=
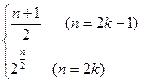
(2)bn=
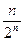 Sn=1
Sn=1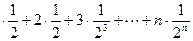 由错位相减得:Sn=2-
由错位相减得:Sn=2-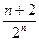

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
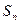 为{an}的前n项和,令bn=anan+1,数列
为{an}的前n项和,令bn=anan+1,数列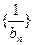 的前n项和为Tn.(1)求an和Sn;(2)求证:Tn<
的前n项和为Tn.(1)求an和Sn;(2)求证:Tn<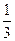 ;(3)是否存在正整数m , n ,且1<m<n ,使得T1 , Tm , Tn成等比数列?若存在,求出m ,n的值,若不存在,说明理由.
;(3)是否存在正整数m , n ,且1<m<n ,使得T1 , Tm , Tn成等比数列?若存在,求出m ,n的值,若不存在,说明理由.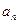 }是等差数列,求证:数列{
}是等差数列,求证:数列{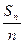 }是等差数列.
}是等差数列.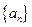 中,
中, 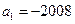 ,其前
,其前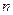 项的和为
项的和为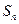 ,若
,若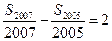 ,求
,求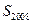 .
.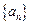 的前
的前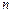 项和为
项和为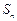 ,通项公式为
,通项公式为 ,
,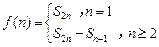 .(Ⅰ)计算
.(Ⅰ)计算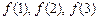 的值;(Ⅱ)比较
的值;(Ⅱ)比较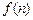 与1的大小,并用数学归纳法证明你的结论.
与1的大小,并用数学归纳法证明你的结论.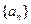 的公比为
的公比为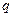 ,前
,前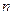 项和为
项和为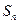 ,若
,若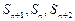 成等差数列,则
成等差数列,则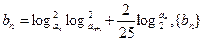 的前n项和为Tn,求
的前n项和为Tn,求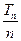 的最小值.
的最小值.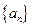 的公差为
的公差为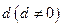 ,且
,且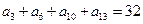 ,若
,若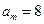 ,则
,则 为
为