题目内容
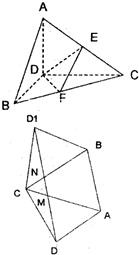
如图,在Rt△ABC中,∠ACB=90°,AC=BC=4,D是AB中点,E是AC的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
(1)求异面直线AB与DE所成的角;
(2)若M,N分别为棱AC,BC上的动点,求△DMN周长的平方的最小值;
(3)在三棱锥D-ABC的外接球面上,求A,B两点间的球面距离和外接球体积.

(1)求异面直线AB与DE所成的角;
(2)若M,N分别为棱AC,BC上的动点,求△DMN周长的平方的最小值;
(3)在三棱锥D-ABC的外接球面上,求A,B两点间的球面距离和外接球体积.

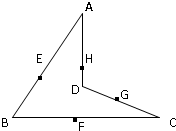
(1)取BC的中点F,连EF,DF则AB∥EF,AB与DE所成角即为EF与DE所成角
∵AD=BD=2
,∠ADB=90°,∴AB=4∴EF=2
又∵DE=DF=2,∴异面直线AB与DE所成角为60°
(2)如图,以C为顶点的侧面展开图,依题意即求DD1的长
∵∠ACD=∠BCD=45°,AC=BC=AB,∴∠ACB=60°
∴∠DCD1=150°,CD=CD1=2
∴D
=(2
)2+(2
)2-2
•2
cos150°=16+8
(3)∵2R=
=2
,∴R=
,V=
πR3=8
π∵AB=4,R=
,∴cosθ=
=-
∴θ=π-arccos
,∴A,B两点的球面距离为(π-arccos
)•
∵AD=BD=2
| 2 |
又∵DE=DF=2,∴异面直线AB与DE所成角为60°
(2)如图,以C为顶点的侧面展开图,依题意即求DD1的长
∵∠ACD=∠BCD=45°,AC=BC=AB,∴∠ACB=60°
∴∠DCD1=150°,CD=CD1=2
| 2 |
∴D
| D | 21 |
| 2 |
| 2 |
| 2 |
| 2 |
| 3 |
(3)∵2R=
3•(2
|
| 6 |
| 6 |
| 4 |
| 3 |
| 6 |
| 6 |
(
| ||||
2•
|
| 1 |
| 3 |
∴θ=π-arccos
| 1 |
| 3 |
| 1 |
| 3 |
| 6 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目