题目内容
【题目】已知袋中装有红球,黑球共7个,若从中任取两个小球(每个球被取到的可能性相同),其中恰有一个红球的概率为![]() .
.
(1)求袋中红球的个数;
(2)若袋中红球比黑球少,从袋中任取三个球,求三个球中恰有一个红球的概率.
【答案】(1)3个或4个 (2)![]()
【解析】
(1)设袋中红球的个数为x,黑球个数为![]() ,根据分步计数原理求出基本事件总数以及恰有一个红球包含的基本事件数,解方程即可求出答案;
,根据分步计数原理求出基本事件总数以及恰有一个红球包含的基本事件数,解方程即可求出答案;
(2)根据计数原理求出恰有一个红球的基本事件数与基本事件总数,再根据概率计算公式求解即可.
解:(1)设袋中红球的个数为x,黑球个数为![]() ,则:
,则:
总的基本事件个数![]() ,
,
取出一个红球的基本事件个数为![]() ,
,
∴![]() ,化简得
,化简得![]() ,
,
解得![]() 或
或![]() ,
,
∴袋中红球的个数为3个或4个;
(2)由(1)可知袋中有3个红球,4个黑球,
基本事件总数为![]() ,
,
①第一次取红球包含的基本事件数为:![]() ,
,
②第二次取红球包含的基本事件数为:![]() ,
,
③第三次取红球包含的基本事件数为:![]() ,
,
∴所求概率![]() .
.

练习册系列答案
相关题目
【题目】自贡农科所实地考察,研究发现某贫困村适合种植![]() ,
,![]() 两种药材,可以通过种植这两种药材脱贫.通过大量考察研究得到如下统计数据:药材
两种药材,可以通过种植这两种药材脱贫.通过大量考察研究得到如下统计数据:药材![]() 的亩产量约为300公斤,其收购价格处于上涨趋势,最近五年的价格如下表:
的亩产量约为300公斤,其收购价格处于上涨趋势,最近五年的价格如下表:
编号 | 1 | 2 | 3 | 4 | 5 |
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
单价(元/公斤) | 18 | 20 | 23 | 25 | 29 |
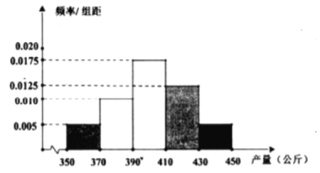
药材![]() 的收购价格始终为20元/公斤,其亩产量的频率分布直方图如下:
的收购价格始终为20元/公斤,其亩产量的频率分布直方图如下:
(1)若药材![]() 的单价
的单价![]() (单位:元/公斤)与年份编号
(单位:元/公斤)与年份编号![]() 具有线性相关关系,请求出
具有线性相关关系,请求出![]() 关于
关于![]() 的回归直线方程,并估计2020年药材
的回归直线方程,并估计2020年药材![]() 的单价;
的单价;
(2)用上述频率分布直方图估计药材![]() 的平均亩产量,若不考虑其他因素,试判断2020年该村应种植药材
的平均亩产量,若不考虑其他因素,试判断2020年该村应种植药材![]() 还是药材
还是药材![]() ?并说明理由.
?并说明理由.
参考公式: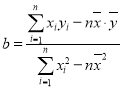 ,
,![]() (回归方程
(回归方程![]() 中)
中)