题目内容
已知函数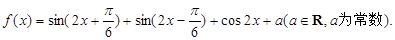 (1)求函数的周期;(2)求函数的单调递增区间;(3)若
(1)求函数的周期;(2)求函数的单调递增区间;(3)若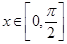 时,
时,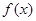 的最小值为– 2 ,求a的值.
的最小值为– 2 ,求a的值.
(1)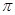 ;(2)
;(2)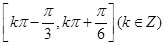 ;(3)a=-1.
;(3)a=-1.
解析试题分析:(1)将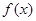 做如下变形:
做如下变形: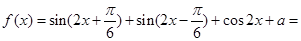
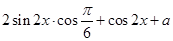
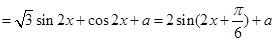 ,
,
根据正弦型函数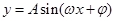 的性质,最小正周期T=
的性质,最小正周期T=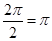 ;(2)根据正弦函数
;(2)根据正弦函数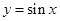 的单调递增区间为
的单调递增区间为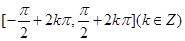 ,可令
,可令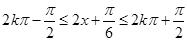
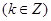 ,解得:
,解得: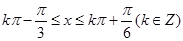 ,从而可以得到
,从而可以得到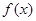 的单调递增区间为
的单调递增区间为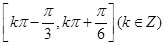 ;
;
(3)当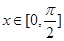 时,
时,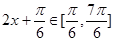 ,∴当
,∴当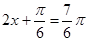 时,
时,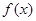 取最小值,结合条件最小值为-2,即可得到有关a的方程,从而求得a=-1.
取最小值,结合条件最小值为-2,即可得到有关a的方程,从而求得a=-1.
(1)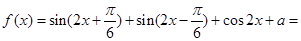
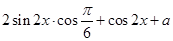
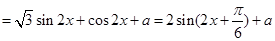 3分
3分
∴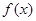 的最小正周期T=
的最小正周期T=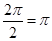 4分
4分
(2) 令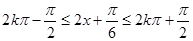
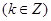 ,解得:
,解得: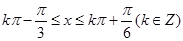 5分
5分
即当函数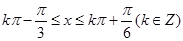 使
使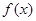 单调递增,
单调递增,
故所求单调递增区间为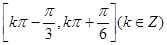 ........7分;
........7分;
(3)∵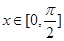 ,∴
,∴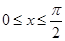 ,∴
,∴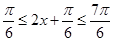 ,∴当
,∴当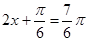 时,
时,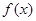 取最小值 9分
取最小值 9分
又∵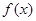 的最小值为-2,∴
的最小值为-2,∴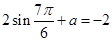 ,∴a="-1" 10分
,∴a="-1" 10分
考点:1、正弦型函数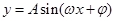 的性质;2、三角函数的单调性;3、三角函数的值域.
的性质;2、三角函数的单调性;3、三角函数的值域.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 图象的一部分如图所示.
图象的一部分如图所示.
 的解析式;
的解析式; 时,求函数
时,求函数 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值.
 x﹣
x﹣ ),x∈R.
),x∈R. ,f(3
,f(3 )=
)=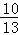 ,f(3β+
,f(3β+ )=
)= .求sin(α+β)的值.
.求sin(α+β)的值.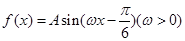 相邻两个对称轴之间的距离是
相邻两个对称轴之间的距离是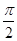 ,且满足,
,且满足,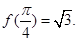
 的单调递减区间;
的单调递减区间; ,求△ABC的面积。
,求△ABC的面积。
 时,求
时,求 的值;
的值;  在
在 上的值域.
上的值域.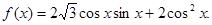
 的值;
的值; 时,求函数
时,求函数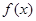 的值域.
的值域. ,cosωx),b=(sinωx,1),函数f(x)=a·b,且最小正周期为4π.
,cosωx),b=(sinωx,1),函数f(x)=a·b,且最小正周期为4π. ,f
,f =
= ,f
,f =-
=- ,求sin(α+β)的值.
,求sin(α+β)的值.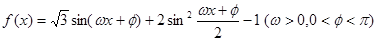 为奇函数,且相邻两对称轴间的距离为
为奇函数,且相邻两对称轴间的距离为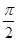 .
.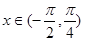 时,求
时,求 的单调递减区间;
的单调递减区间; 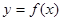 的图象沿
的图象沿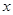 轴方向向右平移
轴方向向右平移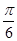 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的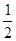 (纵坐标不变),得到函数
(纵坐标不变),得到函数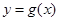 的图象.当
的图象.当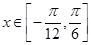 时,求函数
时,求函数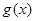 的值域.
的值域.