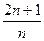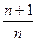题目内容
数列{an}的前n项和为Sn,a1=1,an+1-an-1=0,数列{bn}满足b1=2,anbn+1=2an+1bn.
(1)求S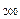 ;
;
(2)求bn.
(1)求S
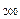 ;
; (2)求bn.
(1)20 100(2)bn=n·2n
(1)∵an+1-an-1=0,∴an+1-an=1.
∴数列{an}是以a1=1为首项,d=1为公差的等差数列.
∴S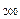 =200×1+
=200×1+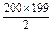 ×1="20" 100.
×1="20" 100.
(2)由(1)得an=n,∴nbn+1=2(n+1)bn.∴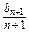 =2·
=2·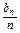 .
.
∴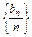 是以
是以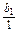 =2为首项,q=2为公比的等比数列.
=2为首项,q=2为公比的等比数列.
∴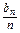 =2×2n-1.∴bn=n·2n.
=2×2n-1.∴bn=n·2n.
∴数列{an}是以a1=1为首项,d=1为公差的等差数列.
∴S
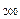 =200×1+
=200×1+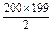 ×1="20" 100.
×1="20" 100.(2)由(1)得an=n,∴nbn+1=2(n+1)bn.∴
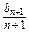 =2·
=2·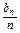 .
.∴
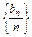 是以
是以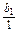 =2为首项,q=2为公比的等比数列.
=2为首项,q=2为公比的等比数列.∴
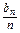 =2×2n-1.∴bn=n·2n.
=2×2n-1.∴bn=n·2n.
练习册系列答案
相关题目
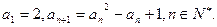
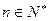 时,恒有
时,恒有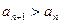 成立;
成立;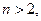 且
且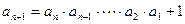 成立;
成立;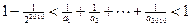 .
.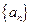 定义如下:
定义如下: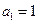 ,且当
,且当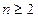 时,
时,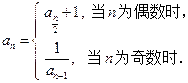
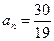 ,求正整数n.
,求正整数n.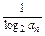 ,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得对于任意的正整数n,有Tn>
,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整数k,使得对于任意的正整数n,有Tn>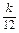 恒成立?若存在,求出k的值;若不存在,说明理由.
恒成立?若存在,求出k的值;若不存在,说明理由.