题目内容
定义数列如下: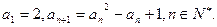
证明:(1)当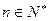 时,恒有
时,恒有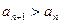 成立;
成立;
(2)当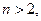 且
且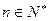 时,有
时,有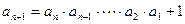 成立;
成立;
(3)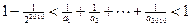 .
.
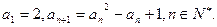
证明:(1)当
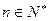 时,恒有
时,恒有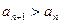 成立;
成立;(2)当
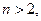 且
且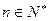 时,有
时,有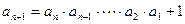 成立;
成立;(3)
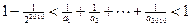 .
.(Ⅰ) 略 (Ⅱ) 见解析 (Ⅲ)见解析
(1)用数学归纳法进行证明.(略)
(2)由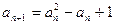 得:
得: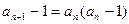
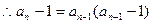 ………
………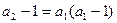
累加得: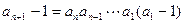
又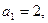 则
则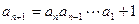
(3)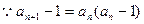
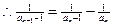

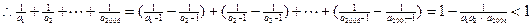
(2)由
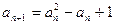 得:
得: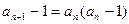
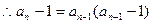 ………
………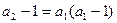
累加得:
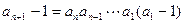
又
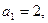 则
则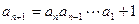
(3)
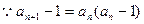
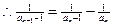

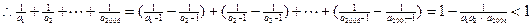

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
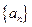 的各项都是正数,
的各项都是正数,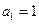 ,
,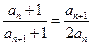 ,
,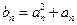 .
.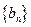 的通项公式;⑵求数列
的通项公式;⑵求数列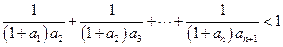 .
.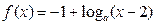 (
(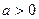 ,且
,且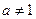 ),
),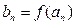 ,
, 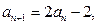 且
且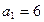 ,
,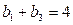
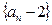 为等比数列
为等比数列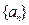 和
和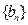 的通项公式。
的通项公式。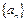 中,
中,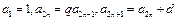 (
(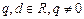 ).
).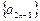 是等比数列,且
是等比数列,且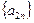 是等差数列,求q, d满足的条件.
是等差数列,求q, d满足的条件. 的值;
的值; ,是否存在一个实数
,是否存在一个实数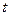 ,使数列
,使数列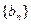 为等差数列?若存在,求出实数
为等差数列?若存在,求出实数 }的前n项和
}的前n项和
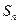
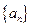

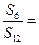
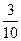
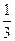

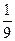
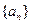 的前
的前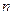 项和为
项和为 ,
,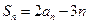 (
(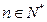 ).
).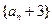 是等比数列,求出数列
是等比数列,求出数列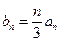 ,求数列
,求数列 的前
的前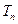 ;
;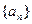 的首项
的首项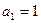 ,公差
,公差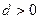 ,且第二项、第五项、第十四项分别是等比数列
,且第二项、第五项、第十四项分别是等比数列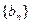 的第二项、第三项、第四项。(1)求数列
的第二项、第三项、第四项。(1)求数列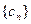 对任意正整数
对任意正整数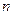 均有
均有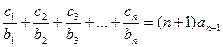 成立,求数列
成立,求数列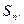
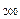 ;
;