题目内容
某林场有荒山3 250亩,每年春季在荒山上植树造林,第一年植树100亩,计划每年比上一年多植树50亩(全部成活)
(1)问需要几年,可将此山全部绿化完?
(2)已知新种树苗每亩的木材量是2立方米,树木每年自然增长率为10%,设荒山全部绿化后的年底的木材总量为S.求S约为多少万立方米?(精确到0.1)
(1)问需要几年,可将此山全部绿化完?
(2)已知新种树苗每亩的木材量是2立方米,树木每年自然增长率为10%,设荒山全部绿化后的年底的木材总量为S.求S约为多少万立方米?(精确到0.1)
需要10年可将此山全部绿化,10年后木材总量约为1.0万立方米.
(1)每年植树的亩数构成一个以a1=100,d=50的等差数列,其和即为荒山的总亩数.
设需要n年可将此山全部绿化,则
Sn=a1n+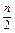 (n-1)d=100n+
(n-1)d=100n+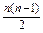 ×50="3" 250.
×50="3" 250.
解此方程,得n=10(年).
(2)第一年种植的树在第10年后的木材量为2a1(1+0.1)10,第二年种植的树在第10年后的木材量为2a2(1+0.1)9,……,
第10年种植的树在年底的木材量为2a10(1+0.1),
第10年后的木材量依次构成数列{bn},则其和为
T=b1+b2+…+b10
=200×1.110+300×1.19+…+1 100×1.1
≈1.0(万立方米).
答 需要10年可将此山全部绿化,10年后木材总量约为1.0万立方米.
设需要n年可将此山全部绿化,则
Sn=a1n+
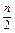 (n-1)d=100n+
(n-1)d=100n+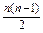 ×50="3" 250.
×50="3" 250.解此方程,得n=10(年).
(2)第一年种植的树在第10年后的木材量为2a1(1+0.1)10,第二年种植的树在第10年后的木材量为2a2(1+0.1)9,……,
第10年种植的树在年底的木材量为2a10(1+0.1),
第10年后的木材量依次构成数列{bn},则其和为
T=b1+b2+…+b10
=200×1.110+300×1.19+…+1 100×1.1
≈1.0(万立方米).
答 需要10年可将此山全部绿化,10年后木材总量约为1.0万立方米.

练习册系列答案
相关题目
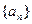 的首项
的首项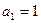 ,公差
,公差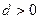 ,且第二项、第五项、第十四项分别是等比数列
,且第二项、第五项、第十四项分别是等比数列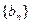 的第二项、第三项、第四项。(1)求数列
的第二项、第三项、第四项。(1)求数列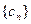 对任意正整数
对任意正整数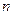 均有
均有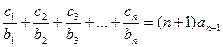 成立,求数列
成立,求数列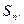
 ;
; 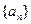 的通项公式为
的通项公式为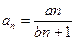 ,其中
,其中 为正数,判断数列
为正数,判断数列