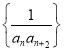题目内容
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调递增区间;
的单调递增区间;
(2)当![]() 时,若函数
时,若函数![]() 有三个不同的零点,求
有三个不同的零点,求![]() 的取值范围;
的取值范围;
(3)设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,当
,当![]() 时,若
时,若![]() 在
在![]() 内恒成立,则称
内恒成立,则称![]() 为函数
为函数![]() 的“类对称点”,请你探究当
的“类对称点”,请你探究当![]() 时,函数
时,函数![]() 是否存在“类对称点”,若存在,请最少求出一个“类对称点” 的横坐标;若不存在,说明理由.
是否存在“类对称点”,若存在,请最少求出一个“类对称点” 的横坐标;若不存在,说明理由.
【答案】(1) 单调递增区间为![]() 和
和![]() ;(2)
;(2) ![]() ; (3)
; (3) ![]() 是一个类对称点的横坐标.
是一个类对称点的横坐标.
【解析】试题分析:(1)求导数f′(x),当a>2时在函数定义域内解不等式f′(x)>0即可.
(2)数形结合:当a=4时,用导数求出函数y=f(x)的极大值与极小值,画出草图,借助图象即可求得m的取值范围.(3)当a=4时,函数y=f(x)在其图象上一点P(x0,f(x0))处的切线方程为y=h(x)=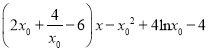 .由此能推导出y=f(x)存在“类对称点”,
.由此能推导出y=f(x)存在“类对称点”, ![]() 是一个“类对称点”的横坐标.
是一个“类对称点”的横坐标.
(1)由![]() 可知,函数的定义域为
可知,函数的定义域为![]() ,
,
且![]() .
.
因为![]() ,所以
,所以![]() .当
.当![]() 或
或![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
所以![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() .
.
(2)当![]() 时,
时, ![]() .所以,当
.所以,当![]() 变化时,
变化时, ![]() 的变化情况如下:
的变化情况如下:
|
| 1 |
| 2 |
|
| + | 0 | - | 0 | + |
| 单调递增 |
| 单调递减 |
| 单调递增 |
所以![]() 极大值
极大值![]() ,
,
![]() 极小值
极小值![]() .
.
函数![]() 的图象大致如下:
的图象大致如下:
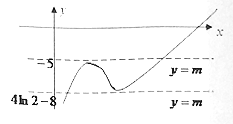
所以若函数![]() 有三个不同的零点,
有三个不同的零点,
则![]() .
.
(3)由题意,当![]() 时,
时, ![]() ,则在点
,则在点![]() 处切线的斜率
处切线的斜率![]() .
.
所以
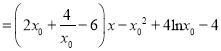 .
.
令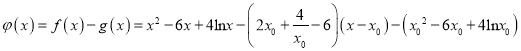 ,
,
则![]() ,
, 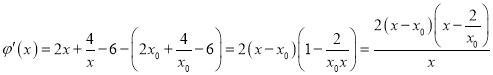 .
.
①当![]() 时,
时, ![]() 在
在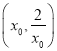 上单调递减,所以当
上单调递减,所以当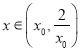 时,
时, ![]() .从而有
.从而有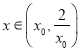 时,
时, ![]() ;
;
②当![]() 时,
时, ![]() 在
在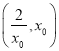 上单调递减,所以当
上单调递减,所以当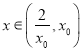 时,
时, ![]() .从而有
.从而有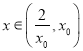 时,
时, ![]() ;
;
所以在![]() 上不存在“类对称点”.
上不存在“类对称点”.
③当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上是增函数,故
上是增函数,故![]() .
.
所以![]() 是一个类对称点的横坐标.
是一个类对称点的横坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目