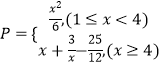题目内容
【题目】已知y=f(x)是R上的可导函数,对于任意的正实数t,都有函数g(x)=f(x+t)﹣f(x)在其定义域内为减函数,则函数y=f(x)的图象可能为如图中( )
A.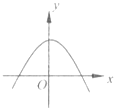
B.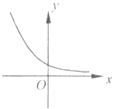
C.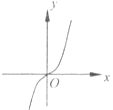
D.
【答案】A
【解析】解:∵函数g(x)=f(x+t)﹣f(x)在其定义域内为减函数, ∴g'(x)=f'(x+t)﹣f'(x)<0在其定义域内恒成立
即f'(x+t)<f'(x),结合t>0,得函数y=f'(x)是其定义域上的减函数.
对于A,可设函数f(x)=ax2+bx+c,(a<0)
∴f'(x)=2ax+b,满足在其定义域上为减函数;
对于B,可设f(x)=ax , (0<a<1)
∴f'(x)=axlna,在(0,+∞)上是增函数,不符合题意;
对于C,可设f(x)=x3 , 可得f'(x)=3x2在其定义域上不是减函数,故C不正确;
对于D,可设f(x)=ax , (a>1)
∴f'(x)=axlna,在(0,+∞)上是增函数,不符合题意.
故选A

练习册系列答案
相关题目