题目内容
【题目】已知α是三角形的内角，且sinα+cosα= 
．
（1）求cos2α的值；
（2）把 
用tanα表示出来，并求其值．
【答案】
（1）解：联立得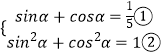 
，
由①得cosα= 
﹣sinα，将其代入②，
整理得25sin2α﹣5sinα﹣12=0．
∵α是三角形内角，
∴可得：sinα= 
，cosα=﹣ 
．
cos2α=2cos2α﹣1=2× 
﹣1=﹣ 
（2）解： 
= 
= 
，
∵tanα=﹣ 
，
∴ = 
=﹣ 
【解析】（1）联立得 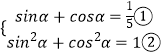，整理得25sin2α﹣5sinα﹣12=0，即可解得sinα，cosα的值，进而利用二倍角的余弦函数公式即可计算得解．（2）利用同角三角函数基本关系式可求 = ，由（1）可求tanα=﹣ ，即可计算得解．
【考点精析】掌握同角三角函数基本关系的运用是解答本题的根本，需要知道同角三角函数的基本关系：
；
;（3） 倒数关系：
．
练习册系列答案
相关题目
