ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌФГГЧЪагавЛПщАыОЖЮЊ40mЕФАыдВаЮЃЈвдOЮЊдВаФЃЌABЮЊжБОЖЃЉТЬЛЏЧјгђЃЌЯжМЦЛЎЖдЦфНјааИФНЈЃЎдкABЕФбгГЄЯпЩЯШЁЕуDЃЌЪЙODЃН80mЃЌдкАыдВЩЯбЁЖЈвЛЕуCЃЌИФНЈКѓЕФТЬЛЏЧјгђгЩЩШаЮЧјгђAOCКЭШ§НЧаЮЧјгђCODзщГЩЃЌЦфУцЛ§ЮЊS m2. ЩшЁЯAOCЃНx rad.
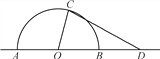
ЃЈ1ЃЉаДГіSЙигкxЕФКЏЪ§ЙиЯЕЪНS(x)ЃЌВЂжИГіxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉеХЧПЭЌбЇЫЕЃКЕБЁЯAOC=![]() ЪБЃЌИФНЈКѓЕФТЬЛЏЧјгђУцЛ§SзюДѓЃЎеХЧПЭЌбЇЕФЫЕЗЈе§ШЗТ№ЃПШєВЛе§ШЗЃЌЧыЧѓГіИФНЈКѓЕФТЬЛЏЧјгђУцЛ§SзюДѓжЕ.
ЪБЃЌИФНЈКѓЕФТЬЛЏЧјгђУцЛ§SзюДѓЃЎеХЧПЭЌбЇЕФЫЕЗЈе§ШЗТ№ЃПШєВЛе§ШЗЃЌЧыЧѓГіИФНЈКѓЕФТЬЛЏЧјгђУцЛ§SзюДѓжЕ.
ЁОД№АИЁПЃЈ1ЃЉSЃН![]() ЃКЃЈ2ЃЉ
ЃКЃЈ2ЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЧѓГіЩШаЮЧјгђAOCЁЂШ§НЧаЮЧјгђCODЕФУцЛ§ЃЌМДПЩЧѓГіSЙигкxЕФКЏЪ§ЙиЯЕЪН![]() ЃЌВЂжИГіxЕФШЁжЕЗЖЮЇЃЛЃЈ2ЃЉЧѓЕМЪ§ЃЌШЗЖЈКЏЪ§ЕФЕЅЕїадЃЌМДПЩЕУГіНсТлЃЎ
ЃЌВЂжИГіxЕФШЁжЕЗЖЮЇЃЛЃЈ2ЃЉЧѓЕМЪ§ЃЌШЗЖЈКЏЪ§ЕФЕЅЕїадЃЌМДПЩЕУГіНсТлЃЎ
ЪдЬтНтЮіЃК
ЃЈ1ЃЉвђЮЊЩШаЮAOCЕФАыОЖЮЊ40mЃЌЁЯAOCЃНx radЃЌ
дк![]() жаЃЌ
жаЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
Ыљвд![]() ЃЎ
ЃЎ
ДгЖј![]()
![]() ЃЋ
ЃЋ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉеХЧПЭЌбЇЕФЫЕЗЈВЛе§ШЗ.
РэгЩШчЯТЃК
гЩЃЈ1ЃЉжЊЃЌ ![]() .
.
![]() .
.
гЩ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() .
.
ДгЖјЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() .
.
вђДЫ![]() дкЧјМф
дкЧјМф![]() ЩЯЕЅЕїЕндіЃЌдкЧјМф
ЩЯЕЅЕїЕндіЃЌдкЧјМф![]() ЩЯЕЅЕїЕнМѕЃЎ
ЩЯЕЅЕїЕнМѕЃЎ
ЫљвдЕБ![]() ЪБЃЌSШЁЕУзюДѓжЕ
ЪБЃЌSШЁЕУзюДѓжЕ![]() ЃЎ
ЃЎ