题目内容
如图,已知抛物线方程为y2=8x.直线l1过抛物线的焦点F,且倾斜角为45°,直线l1与抛物线相交于C、D两点,O为原点.
(1)写出直线l1方程
(2)求CD的长度.
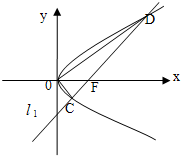
(1)写出直线l1方程
(2)求CD的长度.

(1)由题意可得,抛物线为y2=8x的焦点为(2,0)
∴直线线l1方程为y=x-2即x-y-2=0
(2)联立方程
可得x2-12x+4=0
设C(x1,y1),D(x2,y2)
则x1+x2=12
由抛物线的焦半径公式可得CD=CF+FD=x1+
p+x2+
p=12+4=16
∴直线线l1方程为y=x-2即x-y-2=0
(2)联立方程
|
设C(x1,y1),D(x2,y2)
则x1+x2=12
由抛物线的焦半径公式可得CD=CF+FD=x1+
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
相关题目