Question

已知椭圆

x2

a2

+

y2

b2

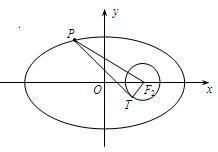
=1（a＞b＞0）的左、右焦点分别为F₁、F₂，焦距为2c；若以F₂为圆心，b-c为半径作圆F₂，过椭圆上任一点P（x₀，y₀）作此圆的切线，切点为T，且|PT|的最小值不小于

3

2

（a-c）．
（Ⅰ）证明：|PF₂|的最小值为a-c；
（Ⅱ）求椭圆的离心率e的取值范围；
（Ⅲ）若椭圆的短半轴长为1，圆F₂与x轴的右交点为Q，过点Q作斜率为2的直线l与椭圆交于A、B两点，若OA⊥OB，求椭圆的方程．

Answer 1

（Ⅰ）证明：设椭圆上任一点Q的坐标为（x₀，y₀），
Q点到右准线的距离为d=

a2

c

-x₀，
则由椭圆的第二定义知：

|QF2|

d

=

c

a

，
∴|QF₂|=a-

c

a

x₀，又-a≤x₀≤a，
∴当x₀=a时，
∴|QF₂|_min=a-c．
（Ⅱ）依题意设切线长|PT|=

|PF2|2-(b-c)2

∴当且仅当|PF₂|取得最小值时|PT|取得最小值，
∴

(a-c)2-(b-c)2

≥

3

2

（a-c），
∴0＜

b-c

a-c

≤

1

2

，从而解得

3

5

≤e＜

2

2

；
（Ⅲ）依题意Q点的坐标为（1，0），则直线的方程为y=2（x-1），
与椭圆方程

x2

a2

+y2=1联立方程组，消去y得（4a²+1）^_x2-8a²x+3a²=0
设A（x₁，y₁）（x₂，y₂），则有x₁+x₂=

8a2

4a2+1

，x₁x₂=

3a2

4a2+1

，
代入直线方程得y₁y₂=

4-4a2

4a2+1

，
∵OA⊥OB，
∴x₁x₂+y₁y₂=0
∴

3a2

4a2+1

+

4-4a2

4a2+1

=0
∴a=2
∴椭圆方程为

x2

4

+y2=1．