题目内容
6. 在四边形ABCD中,AB=$\sqrt{3}$,BC=CD=DA=1,△ABD和△BCD的面积分别为m,n.
在四边形ABCD中,AB=$\sqrt{3}$,BC=CD=DA=1,△ABD和△BCD的面积分别为m,n.(1)若tanA=$\sqrt{2}$,求角C的大小;
(2)求m2+n2的最大值.
分析 (1)根据tanA的值,求得cosA的值,进而利用余弦定理求得BD,确定三边的关系,利用勾股定理判断出C为直角.
(2)利用BD和余弦定理求得cosA和cosC的关系式,进而利用三角形面积公式分别表示出m和n,进而表示出m2+n2,转化为关于cosA的一元二次函数确定函数的最大值.
解答 解:(1)∵tanA=$\sqrt{2}$,
∴cosA=$\frac{\sqrt{3}}{3}$,
BD2=AD2+AB2-2AD•AB•cosA=1+3-2×1×$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=2,
∴BD=$\sqrt{2}$,
∴CD2+BC2=BD2,
∴C=$\frac{π}{2}$.
(2)∵m=$\frac{1}{2}$•AB•AD•sinA=$\frac{\sqrt{3}}{2}$sinA,n=$\frac{1}{2}$•CD•BC•sinC=$\frac{1}{2}$sinC,
∵BD2=AD2+AB2-2AD•AB•cosA=4-2$\sqrt{3}$cosA,
BD2=CD2+BC2-2CD•BC•cosC=2-2cosC,
∴4-2$\sqrt{3}$cosA=2-2cosC,
cosC=$\sqrt{3}$cosA-1,
m2+n2=$\frac{3}{4}$sin2A+$\frac{1}{4}$sin2C=$\frac{3}{4}$(1-cos2A)+$\frac{1}{4}$(1-cos2C)=1-$\frac{3}{4}$cos2A-$\frac{1}{4}$cos2C=1-$\frac{3}{4}$cosA-$\frac{1}{4}$($\sqrt{3}$cosA-1)2=-$\frac{3}{2}$(cosA-$\frac{\sqrt{3}}{6}$)2+$\frac{7}{8}$
∴当cosA=$\frac{\sqrt{3}}{6}$,m2+n2取最大值$\frac{7}{8}$.
点评 本题主要考查了余弦定理的应用.第二步解题关键是利用BD作为桥梁,把两个三角形的等量关系建立联系.

| A. | 命题“?x∈R,x2-x+1≥$\frac{3}{4}$”的否定是“?x0∈R,x02-x0+1<$\frac{3}{4}$” | |
| B. | 命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” | |
| C. | 命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0” | |
| D. | 若命题“非p”与命题“p或q”都是真命题,那么q一定是假命题 |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
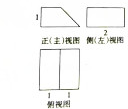
| A. | 2 | B. | 3 | C. | 6 | D. | 9 |