题目内容
11.已知f(α)=$\frac{sin(π+α)cos(2π-α)tan(-α)}{tan(-π-α)sin(-π-α)}$.(1)化简f(α);
(2)若α是第三象限的角,且sin(α-π)=$\frac{1}{5}$,求f(α)的值;
(3)若α=-$\frac{31π}{5}$,求f(α)的值.
分析 (1)直接利用诱导公式化简;
(2)由已知求出sinα的值,然后利用平方关系求得f(α)的值;
(3)把α=-$\frac{31π}{5}$代入f(α)=-cosα化简得答案.
解答 解:(1)f(α)=$\frac{sin(π+α)cos(2π-α)tan(-α)}{tan(-π-α)sin(-π-α)}$=$\frac{-sinα•cosα•(-tanα)}{(-tanα)•sinα}=-cosα$;
(2)由sin(α-π)=$\frac{1}{5}$,得$-sinα=\frac{1}{5}$,sin$α=-\frac{1}{5}$,
又α是第三象限的角,∴f(α)=-cosα=-(-$\sqrt{1-(-\frac{1}{5})^{2}}$)=$\frac{2\sqrt{6}}{5}$;
(3)∵α=-$\frac{31π}{5}$,∴f(α)=-cos(-$\frac{31π}{5}$)=-cos$\frac{π}{5}$.
点评 本题考查了三角函数的化简与求值,关键是对诱导公式的记忆与应用,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.设集合A={x|2x<1},B={x|x2-1≤0},则A∩B=( )
| A. | [-1,0] | B. | (-1,0) | C. | [-1,0) | D. | (-1,0] |
16.已知f(x)为偶函数,当x≥0时,f(x)=m(|x-2|-1)(m>0),若函数y=f[f(x)]恰有4个零点,则m的取值范围为( )
| A. | (0,1) | B. | (1,3) | C. | (1,+∞) | D. | (3,+∞) |
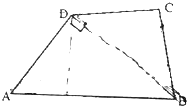 在四边形ABCD中,AB=$\sqrt{3}$,BC=CD=DA=1,△ABD和△BCD的面积分别为m,n.
在四边形ABCD中,AB=$\sqrt{3}$,BC=CD=DA=1,△ABD和△BCD的面积分别为m,n.