题目内容
14.已知有序数对(a,b)∈{(a,b)|a∈[0,4],b∈[0,4]},则方程x2-2ax+b=0有实根的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
分析 根据条件求出a,b对应的平面区域,利用几何概型的概率公式即可得到结论
解答 解:在区间(0,2)上随机取两个数a和b,则$\left\{\begin{array}{l}{0<a<4}\\{0<b<4}\end{array}\right.$,对应的区域面积面积S=4×4=16,
关于x的方程x2-2ax+b=0有实根,
则△=4a2-4b≥0,
即a2≥b≥0,对应的区域为△OABC,
则阴影部分的面积S=${∫}_{0}^{2}{x}^{2}dx$+2×4=$\frac{32}{3}$.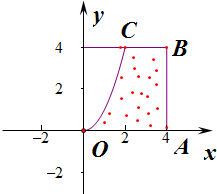
作出不等式组对应的平面区域,根据几何概型的概率公式可知所求的概率为:$\frac{\frac{32}{3}}{16}=\frac{2}{3}$,
故选C.
点评 本题主要考查几何概型的概率计算,作出对应的平面区域,求出相应的面积是解决本题的关键

练习册系列答案
相关题目
19.设集合A={x|2x<1},B={x|x2-1≤0},则A∩B=( )
| A. | [-1,0] | B. | (-1,0) | C. | [-1,0) | D. | (-1,0] |
4.做一个圆柱形锅炉,容积为V,两个底面的材料每单位面积的价格为a元,侧面的材料每单位面积的价格为b元,当造价最低时,锅炉的高与底面直径的比为( )
| A. | $\frac{a}{b}$ | B. | $\frac{{a}^{2}}{b}$ | C. | $\frac{b}{a}$ | D. | $\frac{{b}^{2}}{a}$ |
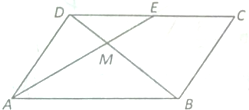
 在四边形ABCD中,AB=$\sqrt{3}$,BC=CD=DA=1,△ABD和△BCD的面积分别为m,n.
在四边形ABCD中,AB=$\sqrt{3}$,BC=CD=DA=1,△ABD和△BCD的面积分别为m,n.