Question

【题目】“既要金山银山，又要绿水青山”。某风景区在一个直径为米的半圆形花圆中设计一条观光线路。打算在半圆弧上任选一点（与不重合），沿修一条直线段小路，在路的两侧（注意是两侧）种植绿化带；再沿弧修一条弧形小路，在小路的一侧（注意是一侧）种植绿化带，小路与绿化带的宽度忽略不计。

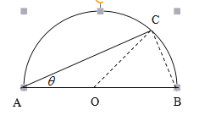
（1）设（弧度），将绿化带的总长度表示为的函数；

（2）求绿化带的总长度的最大值。

Answer 1

【答案】（1），其中；（2）米

【解析】

(1)先设圆心为，连结，根据题意表示出与弧，即可得出；

(2)根据(1)的结果，对函数求导，利用导数方法研究的单调性，进而可求出结果.

（1）设圆心为，连结。

在直角中，，弧的长；

所以，其中。

（2），，

令，可得，所以。

当时，，单调递增；

当时，，单调递减；

所以。

所以绿化带的总长度的最大值为米。