Question

【题目】已知定义域为的函数是奇函数.

（1）求实数的值；

（2）判断的单调性并用定义证明；

（3）已知不等式恒成立, 求实数的取值范围.

Answer 1

【答案】（1）； （2）减函数，证明见解析； （3） .

【解析】

（1）根据奇函数的定义域若存在x=0，则f（0）=0，求解参数的值；

（2）结合y=2x的性质，通过证明任意，有，证明函数是减函数；

（3）根据函数的奇偶性，将不等式恒成立转化为不等式恒成立，再结合函数的单调性求解.

（1）是上的奇函数,， 得

（2）减函数，证明如下：

设是上任意两个实数，且，

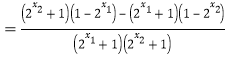
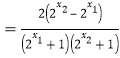
，即， ，

，即，在上是减函数

（3）不等式恒成立，

是奇函数，即不等式恒成立

又 在上是减函数，不等式恒成立

当时，得

当时，得

综上，实数的取值范围是