题目内容
已知椭圆C的中心在原点,焦点在x轴上.若椭圆上的点A(1,
)到焦点F1、F2的距离之和等于4.
(1)写出椭圆C的方程和焦点坐标.
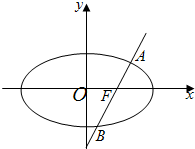
(2)过点Q(1,0)的直线与椭圆交于两点M、N,当△OMN的面积取得最大值时,求直线MN的方程.
| ||
| 2 |
(1)写出椭圆C的方程和焦点坐标.
(2)过点Q(1,0)的直线与椭圆交于两点M、N,当△OMN的面积取得最大值时,求直线MN的方程.
(1)设椭圆的方程为
+
=1(a>b>0)
∵椭圆上的点A(1,
)到焦点F1、F2的距离之和等于4,
∴
,
∴a=2,b=1
∴c=
=
∴椭圆C的方程为
+y2=1,焦点坐标为(-
,0),(
,0);
(2)MN斜率不为0,设MN方程为x=my+1.
联立椭圆方程:
+y2=1可得(m2+4)y2+2my-3=0
记M、N纵坐标分别为y1、y2,
则S△OMN=
|OQ|×|y1-y2|=
×1×
=
设t=
(t≥3)
则S=
=
(t≥
),该式在[
,+∞)单调递减,
∴在t=
,即m=0时S取最大值
.
综上,直线MN的方程为x=1.
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆上的点A(1,
| ||
| 2 |
∴
|
∴a=2,b=1
∴c=
| a2-b2 |
| 3 |
∴椭圆C的方程为
| x2 |
| 4 |
| 3 |
| 3 |
(2)MN斜率不为0,设MN方程为x=my+1.
联立椭圆方程:
| x2 |
| 4 |
记M、N纵坐标分别为y1、y2,
则S△OMN=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| m2+4 |
2
| ||
| m2+4 |
设t=
| m2+3 |
则S=
| 2t |
| t2+1 |
| 2 | ||
t+
|
| 3 |
| 3 |
∴在t=
| 3 |
| ||
| 2 |
综上,直线MN的方程为x=1.

练习册系列答案
相关题目