题目内容
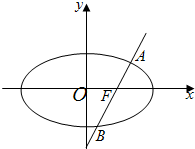
已知椭圆E:
+
=1(a>b>0),过右焦点F且斜率为
的直线l交椭圆E于两点A,B,若以原点为圆心,
为半径的圆与直线l相切
(1)求焦点F的坐标;
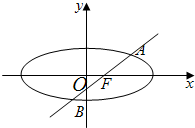
(2)以OA,OB为邻边的平行四边形OACB中,顶点C也在椭圆E上,求椭圆E的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ||
| 3 |
(1)求焦点F的坐标;
(2)以OA,OB为邻边的平行四边形OACB中,顶点C也在椭圆E上,求椭圆E的方程.

(1)F(c,0),直线l的方程为y=
(x-c)
则
=
,所以c=1,所以F(1,0);
(2)设A(x1,y1),B(x2,y2),C(x3,y3),
由已知
=
+
得:x3=x1+x2,y3=y1+y2,
由
⇒(b2+2a2)x2-4a2x+2a2-a2b2=0,
所以
,即
,
点C在椭圆上,所以
+
=1,
整理得:16a2+8b2=(2a2+b2)2,
由
⇒
,
所以椭圆方程为
+
=1.
| 2 |
则
| ||
| 3 |
|
| ||
|
(2)设A(x1,y1),B(x2,y2),C(x3,y3),
由已知
| OC |
| OA |
| OB |
由
|
所以
|
|
点C在椭圆上,所以
(
| ||
| a2 |
(
| ||||
| b2 |
整理得:16a2+8b2=(2a2+b2)2,
由
|
|
所以椭圆方程为
| x2 |
| 3 |
| y2 |
| 2 |


练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目