题目内容
6．求函数f（x）=2x3-3x2-12x+5在区间[-2，3]上的最值．分析 先求出函数f（x）的导数，求出函数的单调区间，从而求出函数的最值．
解答 解：f′（x）=6x2-6x-12，
令f′（x）=0，则6x2-6x-12=0，
即x2-x-2=0，解得x1=-1，x2=2．
列表如下：
| x | -2 | （-2，-1） | -1 | （-1，2） | 2 | （2，3） | 3 |
| f′（x） | + | - | + | ||||
| f（x） | 1 | 递增 | 12 | 递减 | -15 | 递增 | -4 |
点评 本题考查了函数的单调性、最值问题，考查导数的应用，是一道中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
16．若$\overrightarrow a=（2x，1，3），\overrightarrow b=（1，-2y，9）$，若$\overrightarrow a$∥$\overrightarrow b$，则（ ）
| A． | x=1，y=1 | B． | $x=\frac{1}{2}，y=-\frac{1}{2}$ | C． | $x=\frac{1}{6}，y=-\frac{3}{2}$ | D． | $x=-\frac{1}{6}，y=\frac{3}{2}$ |
1．${∫}_{-1}^{1}$x（x-1）的值为（ ）
| A． | 2 | B． | $\frac{2}{3}$ | C． | -$\frac{1}{3}$ | D． | -$\frac{1}{6}$ |
11．函数f（x）=3x3-9x2+5在区间[-2，2]上的最大值是（ ）
| A． | 5 | B． | 2 | C． | -7 | D． | 14 |
把正整数数列的所有数按照从小到大的原则写成如图所示的数表，第k行有k个数，第k行的第s个数（从左数起）记为A（k，s），则2015这个数可记为A（63，62）．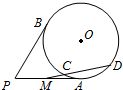
如图，P是圆O外一点，PA，PB是圆O的两条切线，切点分别为A，B，PA中点为M，过M作圆O的一条割线交圆O于C，D两点，若PB=8，MC=2，则CD=6．