题目内容
已知函数f(x)=ax-21nx,a∈R
(Ⅰ)a=1时,求函数f(x)的极值;
(Ⅱ)求f(x)单调区间
(Ⅲ)设g(x)=
(a>0),若在[1,e]上至少存在一个x0,使得f(x0)>g(x0)成立,求实数a的取值范围.
(Ⅰ)a=1时,求函数f(x)的极值;
(Ⅱ)求f(x)单调区间
(Ⅲ)设g(x)=
| a+2e |
| x |
(I)f′(x)=1-
,x>0.令f'(x)=0,得x=2
当x变化时,f'(x)与f(x)变化情况如下表:
∴当x=2时,f(x)取得极小值f(2)=2-2ln2.
(Ⅱ)a≤0时,f(x)在(0,+∞)上为减函数;a>0时,f(x)在(0,
)上是减函数,
在(
,+∞)上是增函数.
(Ⅲ)本命题等价于f(x)-g(x)>0在[1,e]上有解,设F(x)=f(x)-g(x)=ax-2lnx-
,
F'(x)=a-
+
=
=
>0,
所以F(x)为增函数,F(x)max=F(e).
依题意需F(e)>0,解得a>
.所以a的取值范围是(
,+∞).
| 2 |
| x |
当x变化时,f'(x)与f(x)变化情况如下表:
| x | (0,2) | 2 | (2,+∞) |
| f'(x) | - | 0 | + |
| f(x) | 单调递减 | 极小值 | 单调递增 |
(Ⅱ)a≤0时,f(x)在(0,+∞)上为减函数;a>0时,f(x)在(0,
| 2 |
| a |
在(
| 2 |
| a |
(Ⅲ)本命题等价于f(x)-g(x)>0在[1,e]上有解,设F(x)=f(x)-g(x)=ax-2lnx-
| a+2e |
| x |
F'(x)=a-
| 2 |
| x |
| a+2e |
| x2 |
| ax2-2x+a+2e |
| x2 |
| ax2+a+2(e-x) |
| x2 |
所以F(x)为增函数,F(x)max=F(e).
依题意需F(e)>0,解得a>
| 4e |
| e2-1 |
| 4e |
| e2-1 |

练习册系列答案
相关题目
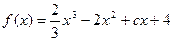 ,
,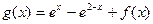 ,
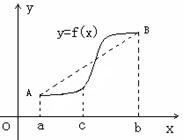
,
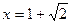 处取得极值,试求c的值和f(x)的单调增区间;
处取得极值,试求c的值和f(x)的单调增区间;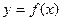 的图象在
的图象在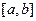 连续光滑,试猜想拉格朗日中值定理:即一定存在
连续光滑,试猜想拉格朗日中值定理:即一定存在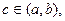 使得
使得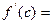 ?(用含有a,b,f(a),f(b)的表达式直接回答)
?(用含有a,b,f(a),f(b)的表达式直接回答)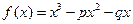 的图象与
的图象与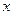 轴切于
轴切于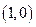 点,求
点,求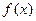 的极值。
的极值。