题目内容
已知f(x)=x3-ax+b-1是定义在R上的奇函数,且在x=
时取最得极值,则a+b的值为( )
| ||
| 3 |
A.
| B.
| C.1 | D.2 |
f(x)=x3-ax+b-1是定义在R上的奇函数,
∴f(-x)=-f(x),化简计算得b=1.
∵函数f(x)在x=
时取得极值,∴f′(
)=0.
又由f′(x)=3x2-a,
∴f′(
)=3×(
)2-a=0,则a=1.
故a+b=2
故答案为 D
∴f(-x)=-f(x),化简计算得b=1.
∵函数f(x)在x=
| ||
| 3 |
| ||
| 3 |
又由f′(x)=3x2-a,
∴f′(
| ||
| 3 |
| ||
| 3 |
故a+b=2
故答案为 D

练习册系列答案
相关题目
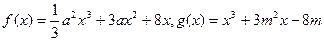 ,
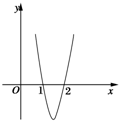
,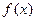 在x=1处的切线斜率的取值范围;
在x=1处的切线斜率的取值范围; ,总存在
,总存在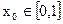 ,使得
,使得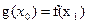 成立?若存在,求出实数m的取值范围;若不存在,说明理由.
成立?若存在,求出实数m的取值范围;若不存在,说明理由.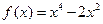 有( )
有( )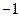 ,极大值
,极大值
 ,极大值
,极大值