题目内容
设函数f(x)=
x3-
x2+(m+1)x+1.
(1)若函数f(x)在x=1处取得极大值,求函数f(x)的单调递增区间;
(2)若对任意实数m∈(0,+∞),不等式f'(x)>x2m2-(x2+1)m+x2-x+1恒成立,求x的取值范围.
| m2 |
| 3 |
| 3 |
| 2 |
(1)若函数f(x)在x=1处取得极大值,求函数f(x)的单调递增区间;
(2)若对任意实数m∈(0,+∞),不等式f'(x)>x2m2-(x2+1)m+x2-x+1恒成立,求x的取值范围.
(1)f′(x)=m2x2-3x+(m+1).
由条件知f′(1)=0
所以m2+m-2=0
故m=1或m=-2
当m=-2时,f(x)在x=1处取得极小值;
当m=1时,f(x)在x=1处取得极大值;
综上可知,m=1
f′(x)=x2-3x+2.
由f′(x)≥0,得x≤1或x≥2;
故f(x)的单调递增区间为(-∞,1],[2,+∞).
(2)由已知知,m2x2-3x+(m+1)>x2m2-(x2+1)m+x2-x+1恒成立.
即m(x2+2)-x2-2x>0对任意m∈(0,+∞)恒成立
由m(x2+2)-x2-2x>0,及x2+2>0,
可知对任意m∈(0,+∞),m>
恒成立.
故
≤0,
又x2+2>0恒成立,
所以,x2+2x≤0,
即-2≤x≤0,
故原不等式恒成立的x的取值范围是-2≤x≤0.
由条件知f′(1)=0
所以m2+m-2=0
故m=1或m=-2
当m=-2时,f(x)在x=1处取得极小值;
当m=1时,f(x)在x=1处取得极大值;
综上可知,m=1
f′(x)=x2-3x+2.
由f′(x)≥0,得x≤1或x≥2;
故f(x)的单调递增区间为(-∞,1],[2,+∞).
(2)由已知知,m2x2-3x+(m+1)>x2m2-(x2+1)m+x2-x+1恒成立.
即m(x2+2)-x2-2x>0对任意m∈(0,+∞)恒成立
由m(x2+2)-x2-2x>0,及x2+2>0,
可知对任意m∈(0,+∞),m>
| x2+2x |
| x2+2 |
故
| x2+2x |
| x2+2 |
又x2+2>0恒成立,
所以,x2+2x≤0,
即-2≤x≤0,
故原不等式恒成立的x的取值范围是-2≤x≤0.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
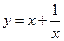 在
在 时有( )
时有( )