题目内容
【题目】如图,在棱长为![]() 的正方体
的正方体![]() 中,
中,![]() 分别为棱
分别为棱![]() 的中点,
的中点,![]() 是线段
是线段![]() 的中点,若点
的中点,若点![]() 分别为线段
分别为线段![]() 上的动点,则
上的动点,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
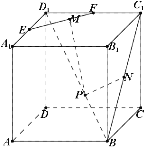
连接B1D1交EF于G,连接PG,则EF⊥平面B1D1DB,故EF⊥PG,从而PM的最小值PG,可知G为EF的中点,D1G为D1B1的四分之一.其次,连接BD,设其中点为H,连接PH,BC1,则△D1DB≌△D1C1B,从而PN=PH.(实现了转化,这步是解题之关键),最后,连接GH交BD1于K,则当P为K时,PM+PN取得最小值,所求最小值为GH,即可得出结论.
首先PM的最小值就是P到EF的距离.
连接B1D1交EF于G,连接PG,则EF⊥平面B1D1DB,故EF⊥PG,从而PM的最小值PG,可知G为EF的中点,D1G为D1B1的四分之一.其次,连接BD,设其中点为H,连接PH,BC1,则△D1DB≌△D1C1B1,从而PN=PH.(实现了转化,这步是解题之关键)
最后,连接GH交BD1于K,则当P为K时,PM+PN取得最小值,所求最小值为GH.
∵正方体ABCD﹣A1B1C1D1的棱长为1,
∴GH=![]() =
=![]() .
.
故选:D.

练习册系列答案
相关题目