题目内容
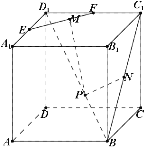
【题目】如图，三棱柱ABC－A1B1C1中，CA＝CB，AB＝AA1，∠BAA1＝60°.
O为AB的中点
(1)证明：AB⊥平面A1OC
(2)若AB＝CB＝2，平面ABC
平面A1ABB1，求三棱柱ABC－A1B1C1的体积．
【答案】(1)见解析；（2）3
【解析】
（1）利用有一个角是
的等腰三角形是等边三角形，证得三角形
是等边三角形，由此证得
，再根据三角形
为等腰三角形证得
，故
平面
.（2）由（1）利用面面垂直的性质定理，证得
平面
，即
为三棱柱的高，由此可求得三棱柱的体积.
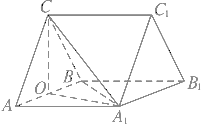
(1)证明：连结A1B.，因为CA＝CB，OA＝OB，所OC⊥AB
因为AB＝AA1，∠BAA1＝60°，所三角形AA1B为等边三角形，
所以AA1＝A1B，又OA＝OB，所以OA1⊥AB，又
＝
，
面A1OC
（2）由题可知，
与
是边长为2的等边三角形，得
平面ABC
平面A1ABB 平面ABC
平面A1ABB＝AB，
由（1）OA1⊥AB，
平面A1ABB
面ABC
为三棱柱ABC－A1B1C
＝3
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】对某校高一年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：
分组 | 频数 | 频率 |
[10，15） | 10 | 0.25 |
[15，20） | 25 | n |
[20，25） | m | p |
[25，30） | 2 | 0.05 |
合计 | M | 1 |
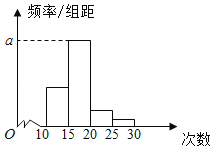
（1）求出表中M，p及图中a的值；
（2）若该校高一学生有360人，试估计该校高一学生参加社区服务的次数在区间[15，20）内的人数；
（3）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，请列举出所有基本事件，并求至多1人参加社区服务次数在区间[20，25）内的概率．
【题目】张三同学从7岁起到13岁每年生日时对自己的身高测量后记录如表：
年龄 （岁） | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
身高 （cm） | 121 | 128 | 135 | 141 | 148 | 154 | 160 |
（Ⅰ）求身高y关于年龄x的线性回归方程；
（Ⅱ）利用（Ⅰ）中的线性回归方程，分析张三同学7岁至13岁身高的变化情况，如17岁之前都符合这一变化，请预测张三同学15岁时的身高．
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
= 
， 
．
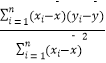【题目】对某校高一年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：
分组 | 频数 | 频率 |
[10，15） | 10 | 0.25 |
[15，20） | 25 | n |
[20，25） | m | p |
[25，30） | 2 | 0.05 |
合计 | M | 1 |
（1）求出表中M，p及图中a的值；
（2）若该校高一学生有360人，试估计该校高一学生参加社区服务的次数在区间[15，20）内的人数；
（3）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，请列举出所有基本事件，并求至多1人参加社区服务次数在区间[20，25）内的概率．
