题目内容
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,倾斜角为α(α≠ ![]() )的直线l的参数方程为
)的直线l的参数方程为 ![]() (t为参数).以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程是ρcos2θ﹣4sinθ=0.
(t为参数).以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程是ρcos2θ﹣4sinθ=0.
(I)写出直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)已知点P(1,0).若点M的极坐标为(1, ![]() ),直线l经过点M且与曲线C相交于A,B两点,设线段AB的中点为Q,求|PQ|的值.
),直线l经过点M且与曲线C相交于A,B两点,设线段AB的中点为Q,求|PQ|的值.
【答案】解:(Ⅰ)∵直线l的参数方程为 ![]() (t为参数). ∴直线l的普通方程为y=tanα(x﹣1),
(t为参数). ∴直线l的普通方程为y=tanα(x﹣1),
由曲线C的极坐标方程是ρcos2θ﹣4sinθ=0,得ρ2cos2θ﹣4ρsinθ=0,
∴x2﹣4y=0,
∴曲线C的直角坐标方程为x2=4y.
(Ⅱ)∵点M的极坐标为(1, ![]() ),∴点M的直角坐标为(0,1),
),∴点M的直角坐标为(0,1),
∴tanα=﹣1,直线l的倾斜角为 ![]() ,
,
∴直线l的参数方程为 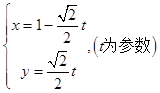 ,
,
代入x2=4y,得 ![]() ,
,
设A,B两点对应的参数为t1 , t2 ,
∵Q为线段AB的中点,
∴点Q对应的参数值为 ![]() ,
,
又P(1,0),则|PQ|=| ![]() |=3
|=3 ![]() .
.
【解析】(Ⅰ)直线l的参数方程消去参数t,能求出直线l的普通方程;由曲线C的极坐标方程能求出曲线C的直角坐标方程.(Ⅱ)求出点M的直角坐标为(0,1),从而直线l的倾斜角为 ![]() ,由此能求出直线l的参数方程,代入x2=4y,得
,由此能求出直线l的参数方程,代入x2=4y,得 ![]() ,由此利用韦达定理和两点间距离公式能求出|PQ|.
,由此利用韦达定理和两点间距离公式能求出|PQ|.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案【题目】张三同学从7岁起到13岁每年生日时对自己的身高测量后记录如表:
年龄 (岁) | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
身高 (cm) | 121 | 128 | 135 | 141 | 148 | 154 | 160 |
(Ⅰ)求身高y关于年龄x的线性回归方程;
(Ⅱ)利用(Ⅰ)中的线性回归方程,分析张三同学7岁至13岁身高的变化情况,如17岁之前都符合这一变化,请预测张三同学15岁时的身高.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:![]() =
= 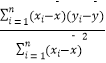 ,
, ![]() .
.