题目内容
【题目】已知椭圆E： 
=1（a＞b＞0）的离心率是 
，过E的右焦点且垂直于椭圆长轴的直线与椭圆交于A，B两点，|AB|=2．
（Ⅰ）求椭圆方程；
（Ⅱ）过点P（0， 
）的动直线l与椭圆E交于的两点M，N（不是的椭圆顶点），是否存在实数λ，使 
+λ 
为定值？若存在，求出λ的值；若不存在，请说明理由．
【答案】解：（Ⅰ）由椭圆的离心率e= 
= 
= 
，则a2=2b2 ， ①
则丨AB丨= 
=2，则b2=a，②
解得：a=2，b= 
，
∴椭圆的标准方程为： 
；
（Ⅱ）当直线AB的斜率存在时，设直线AB的方程为y=kx+ 
，M（x1 ， y1），N（x2 ， y2），
联立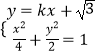 
，得（1+2k2）x2+4 kx+2=0，△=（4 k）2﹣4×（1+2k2）×2＞0，解得：k2＞ 
，
由韦达定理可知：x1+x2=﹣ 
，x1x2= 
，从而， 
+λ 
=x1x2+y1y2+λ[x1x2+（y1﹣ ）（y2﹣ ）]，
=（1+λ）（1+k2）x1x2+ k（x1+x2）+3，
=（1+λ）（1+k2）× + k×（﹣ ）+3，
= 
，
=﹣（1﹣λ）+ 
，
∴当λ=﹣2时，﹣（1﹣λ）+ =﹣3，此时 +λ =﹣3，
故存在常数λ=﹣2，使得 +λ 为定值﹣3．
【解析】（Ⅰ）由题意的离心率求得a2=2b2 ， 椭圆的通径丨AB丨= =2，即可求得a和b的值，求得椭圆的标准方程；（Ⅱ）设直线l的方程，y=kx+ ，代入椭圆方程，利用韦达定理定理及向量数量积的坐标运算，表示出 +λ =﹣（1﹣λ）+ ，则当λ=﹣2时，﹣（1﹣λ）+ =﹣3，则存在实数λ，使 +λ 为定值
【考点精析】本题主要考查了椭圆的标准方程的相关知识点，需要掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
才能正确解答此题．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】对某校高一年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：
分组 | 频数 | 频率 |
[10，15） | 10 | 0.25 |
[15，20） | 25 | n |
[20，25） | m | p |
[25，30） | 2 | 0.05 |
合计 | M | 1 |
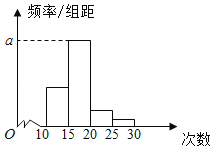
（1）求出表中M，p及图中a的值；
（2）若该校高一学生有360人，试估计该校高一学生参加社区服务的次数在区间[15，20）内的人数；
（3）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，请列举出所有基本事件，并求至多1人参加社区服务次数在区间[20，25）内的概率．
