题目内容
【题目】若函数g(x)满足g(g(x))=n(n∈N)有n+3个解,则称函数g(x)为“复合n+3解”函数.已知函数f(x)= 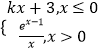 (其中e是自然对数的底数,e=2.71828…,k∈R),且函数f(x)为“复合5解”函数,则k的取值范围是( )
(其中e是自然对数的底数,e=2.71828…,k∈R),且函数f(x)为“复合5解”函数,则k的取值范围是( )
A.(﹣∞,0)
B.(﹣e,e)
C.(﹣1,1)
D.(0,+∞)
【答案】D
【解析】解:函数f(x)为“复合5解“, ∴f(f(x))=2,有5个解,
设t=f(x),
∴f(t)=2,
∵当x>0时,f(x)= ![]() ,
,
∴f(x)= ![]() ,
,
当0<x<1时,f′(x)<0,函数f(x)单调递减,
当x>1时,f′(x)>0,
函数f(x)单调递增,
∴f(x)min=f(1)=1,
∴t≥1,
∴f(t)=2在[1,+∞)有2个解,
当x≤0时,f(x)=kx+3,函数f(x)恒过点(0,3),
当k≤0时,f(x)≥f(0)=3,
∴t≥3
∵f(3)= ![]() >2,
>2,
∴f(t)=2在[3,+∞)上无解,
当k>0时,f(x)≤f(0)=3,
∴f(t)=2,在(0,3]上有2个解,在(∞,0]上有1个解,
综上所述f(f(x))=2在k>0时,有5个解,
故选:D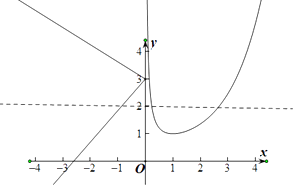

【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |
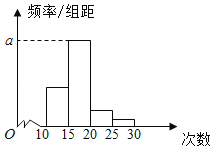
(1)求出表中M,p及图中a的值;
(2)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,请列举出所有基本事件,并求至多1人参加社区服务次数在区间[20,25)内的概率.