题目内容
设函数 ,
, 是定义域为R上的奇函数.
是定义域为R上的奇函数.
(1)求 的值,并证明当
的值,并证明当 时,函数
时,函数 是R上的增函数;
是R上的增函数;
(2)已知 ,函数
,函数 ,
, ,求
,求 的值域;
的值域;
(3)若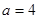 ,试问是否存在正整数
,试问是否存在正整数 ,使得
,使得 对
对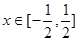 恒成立?若存在,请求出所有的正整数
恒成立?若存在,请求出所有的正整数 ;若不存在,请说明理由.
;若不存在,请说明理由.
(1)如下(2)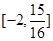 (3)存在正整数
(3)存在正整数 =3或4
=3或4
解析试题分析:解:(1)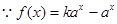 是定义域为R上的奇函数,
是定义域为R上的奇函数,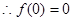 ,得
,得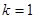 .
.
此时,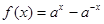 ,
,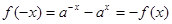 ,即
,即 是R上的奇函数.
是R上的奇函数.
设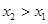 ,则
,则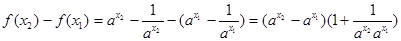 ,
,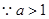 ,
,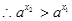 ,
,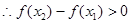 ,
,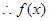 在R上为增函数.
在R上为增函数.
(2)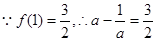 ,即
,即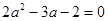 ,
,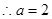 或
或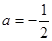 (舍去),
(舍去),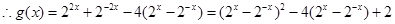
令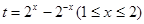 ,由(1)知
,由(1)知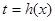 在[1,2]上为增函数,∴
在[1,2]上为增函数,∴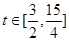 ,
,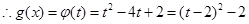 ,
,
当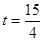 时,
时, 有最大值
有最大值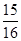 ;当
;当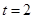 时,
时, 有最小值
有最小值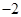 ,
,
∴ 的值域
的值域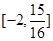 .
.
(3)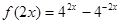 =
=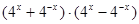 ,
,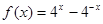 ,
,
假设存在满足条件的正整数 ,则
,则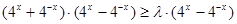 ,
,
①当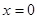 时,
时,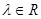 .
.
②当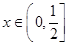 时,
时,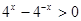 ,则
,则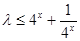 ,令
,令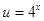 ,则
,则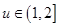 ,易证
,易证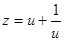 在
在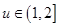 上是增函数,∴
上是增函数,∴ .
.
③当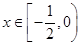 时,
时,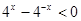 ,则
,则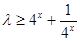 ,令
,令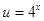 ,则
,则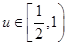 ,易证
,易证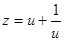 在
在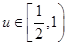 上是减函数,∴
上是减函数,∴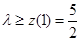 .
.
综上所述,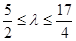 ,∵
,∵ 是正整数,∴
是正整数,∴ =3或4.
=3或4.
∴存在正整数 =3或4,使得
=3或4,使得 对
对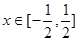 恒成立.
恒成立.
考点:函数的单调性
点评:本题难度较大。函数的单调性对求最值、判断函数值大小关系和证明不等式都有较大帮助,而求函数的单调性有时可以结合导数来求。

2013年,首都北京经历了59年来雾霾天气最多的一个月。经气象局统计,北京市从1月1日至1月30日这30天里有26天出现雾霾天气。《环境空气质量指数(AQI)技术规定(试行)》将空气质量指数分为六级:其中,中度污染(四级),指数为151—200;重度污染(五级),指数为201—300;严重污染(六级),指数大于300. 下面表1是该观测点记录的4天里,AQI指数 与当天的空气水平可见度
与当天的空气水平可见度 (千米)的情况,表2是某气象观测点记录的北京1月1日到1月30日AQI指数频数统计结果,
(千米)的情况,表2是某气象观测点记录的北京1月1日到1月30日AQI指数频数统计结果,
表1:AQI指数 与当天的空气水平可见度
与当天的空气水平可见度 (千米)情况
(千米)情况
AQI指数 |  |  |  |  |
空气可见度 (千米) (千米) |  |  |  |  |
| AQI指数 |  |  |  |  |  |
| 频数 | 3 | 6 | 12 | 6 | 3 |
 ,根据表1的数据,求出
,根据表1的数据,求出 关于
关于 的线性回归方程;
的线性回归方程;(Ⅱ)根据表2估计这30天AQI指数的平均值.
(用最小二乘法求线性回归方程系数公式
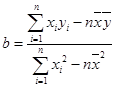 ,
, )
) 有一批货物需要用汽车从生产商所在城市甲运至销售商所在城市乙.已知从城市甲到城市乙只有两条公路,且通过这两条公路所用的时间互不影响.
据调查统计,通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布如下表:
| 所用的时间(天数) | 10 | 11 | 12 | 13 |
| 通过公路1的频数 | 20 | 40 | 20 | 20 |
| 通过公路2的频数 | 10 | 40 | 40 | 10 |
(Ⅰ)为了尽最大可能在各自允许的时间内将货物运往城市乙,估计汽车A和汽车B应如何选择各自的路径;
(Ⅱ)若通过公路1、公路2的“一次性费用”分别为
 万元、
万元、 万元(其它费用忽略不计),此项费用由生产商承担.如果生产商恰能在约定日期当天将货物送到,则销售商一次性支付给生产商40万元,若在约定日期前送到,每提前一天销售商将多支付给生产商2万元;若在约定日期后送到,每迟到一天,销售商将少支付给生产商2万元.如果汽车A、B长期按(Ⅰ)所选路径运输货物,试比较哪辆汽车为生产商获得的毛利润更大.(注:毛利润=(销售商支付给生产商的费用)一(一次性费用)) .
万元(其它费用忽略不计),此项费用由生产商承担.如果生产商恰能在约定日期当天将货物送到,则销售商一次性支付给生产商40万元,若在约定日期前送到,每提前一天销售商将多支付给生产商2万元;若在约定日期后送到,每迟到一天,销售商将少支付给生产商2万元.如果汽车A、B长期按(Ⅰ)所选路径运输货物,试比较哪辆汽车为生产商获得的毛利润更大.(注:毛利润=(销售商支付给生产商的费用)一(一次性费用)) .  是奇函数,
是奇函数, 是偶函数。
是偶函数。 的值;
的值; 若
若 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。 ,及函数
,及函数 。
。 的不等式
的不等式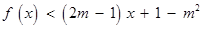 的解集为
的解集为 ,其中
,其中 为正常数。
为正常数。 的值;
的值; R
R 如何取值时,函数
如何取值时,函数

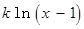 存在极值点,并求出极值点;
存在极值点,并求出极值点; ,且
,且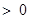 ,求证:
,求证:
 。
。 )万元。
)万元。 百件,生产并销售这种产品得到的利润为当年产量
百件,生产并销售这种产品得到的利润为当年产量 ,求
,求 (元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用
(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用 (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得).
(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得). 的解析式及其定义域;
的解析式及其定义域; 是定义在
是定义在  上的增函数,且对任意的
上的增函数,且对任意的 都满足
都满足 .
. 的值; (Ⅱ)若
的值; (Ⅱ)若 ,证明
,证明 ;
; ,解不等式
,解不等式  .
.